今回よりdeeplearning.ai の深層学習講座のまとめになります。コースは現在までのところ5コース用意されており、4コースが開講されています。
今年の夏に第1のコースNeural Networks and Deep Learning - Coursera を受講したのですが、理解不足で挫折してしまいました。同じアンドリューng先生の機械学習講座 の受講が終わったので再挑戦してみます。
誤差逆伝播法
機械学習講座では省略されていたニューラルネットワークの「誤差逆伝播法」に関して、こちらのコースではかなり詳細に講義がされています。
前回の受講でつまずいたところなのでステップを踏んでまとめてみたいと思います。
計算グラフ(Computation Graph)
スタンフォード大学の講座CS231nでは「誤差逆伝播法」を視覚的に理解するため、数式と合わせて計算グラフによって説明をしているようです。
このディープラーニング講座でも同じように計算グラフを使いながらその手法を理解するように進められます。
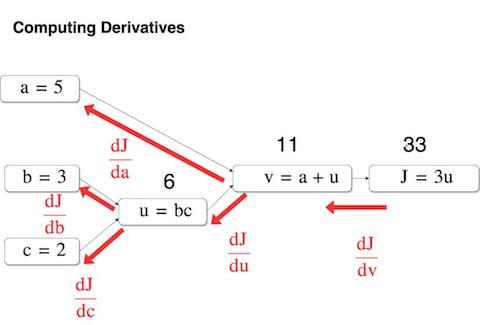
こんな感じです。ノードと呼ばれる計算式とエッジと呼ばれる矢印で計算を視覚的に理解することが出来ます。
ここでは $a, b, c$ 3つの変数をノードによって計算していきます。左から右に計算することを順伝播、左から右に計算することを逆伝播と言います。
なぜ計算グラフを使うのかというと、複雑な計算をノード毎の局所的に計算に置き換えることが出来るからです。それにより逆伝播の微分を効率良く計算することが出来ます。
微分の表し方は複数あるのですが、ここでは関数 $y=f(x)$ を $x$ で微分する、という意味で $f(x) = \frac{dy}{dx}$ という表記を使います。
さて、逆伝播の微分は上の図のように表すことが出来ますが、一つ一つ微分して更新していくのでは計算量が膨大になる為、合成関数(複合関数)と連鎖律という手法を使って計算します。
連鎖律(Chain Rule)
「連鎖律の原理」は次のように表すことが出来ます。
ある関数が合成関数で表される場合、その合成関数の微分は、合成関数を構成するそれぞれの関数の微分の積によって表すことが出来る
ゼロから作るDeep Learning - O’REILLYジャパン より引用
数式で表すと以下の様になります。
$$
\frac{dz}{dx} = \frac{dz}{dt} \frac{dt}{dx}
$$
「連鎖律」の名前の通り、逆伝播の右からの計算が数珠つなぎに左側に計算していく事が可能になります。
上の図で微分 $ \frac{dJ}{da}$ を求める際、こんな計算で求めることが出来ます。
$$
\frac{dJ}{da}=\frac{dJ}{dv}\frac{dv}{da}=3×1=3
$$
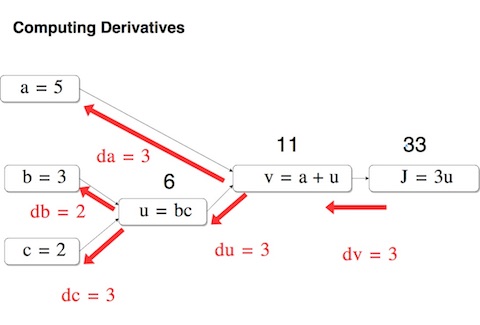
同じ様に連鎖律を使い計算して行くと上図の様になります。( $ \frac{dJ}{da}$ は $da$ の様に省略して記述しています)
今回はここまで。次回はロジスティック回帰の逆伝播を見ていくことにします。