さて、引き続き Machine Learning - Coursera で学習したことのまとめです。
重回帰分析 (Linear Regression with Multiple Variables)
仮説の予測変数 $x$ を1つで考えてきましたが、この予測変数は複数であっても分析することが出来ます。
単回帰に対し、複数予測変数がある場合は重回帰と呼ばれます。
仮説は以下の様に表すことが出来ます。
$$
{
h_\theta (X) = \theta^{\mathrm{T}} X^{\mathrm{T}}
}
$$
ここでの $T$ は転置行列(行と列を入れ替えた行列)と呼ばれます。
重回帰分析の目的関数と最急降下法
目的関数は以下の様に表わせます。
$${ J(\theta) = \frac{1}{2m} \sum_{i=1}^m (h_\theta (x^{(i)}) - y^{(i)})^2 }$$最急降下法は以下の様に表わせます。
$${ \theta_j := \theta_j - \alpha\frac{\partial}{\partial \theta_j}J(\theta) }$$目的関数を最急降下法に代入すると以下の様になります。
$${ \theta_j := \theta_j - \alpha \sum_{i=1}^m (h_\theta (x^{(i)}) - y^{(i)}) x_j ^{(i)} }$$基本式は単回帰の時と同様です。
スケーリング (feature scaling)
複数のベクトルの集合である $X$ は説明変数とも呼ばれます。これらの説明変数の範囲が不均一の場合、勾配降下が非効率に行われます。
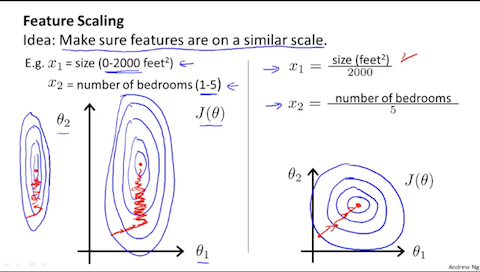
画像引用:Machine Learning - Coursera
特徴選択のスケーリングを行うことでそれは改善されます。
$$
x_i := \dfrac{x_i - \mu_i}{s_i}
$$
$μ_i$ は要素$(i)$の平均値、 $s_i$ は 要素$(i)$ の最大値と最小値の差分(標準偏差)を表します。以下の様にも表すことが出来ます。
$$
{
x_i := \frac{x_i - mean(x)}{max(x) - min(x)}
}
$$
重回帰分析において目的関数の最小値を求めるには正規方程式 (Normal Equation)という方法もありますが、このまとめでは省略します。
では。