さて、今回は分類(Classification)に関して学習したことをまとめてみます。
ロジスティック回帰 (Logistic Regression)
予測値 $y’$ を0.5以上を1とし、0.5未満を0とすることで分類を行います。線形回帰では目的関数の範囲が定まっておらず、分類することが出来ないため、ロジスティック回帰を使います。
ロジスティック関数 (Logistic Function)あるいは、シグモイド関数 (Sigmoid Function)
シグモイド関数(別名:ロジスティック関数) $g(z)$ は以下の様な関数です。
$$
g(z) = \dfrac{1}{1 + e^{-z}}
$$
ロジスティック回帰における仮説 $h_\theta (x)$ はシグモイド関数 $g(z)$ に予測変数 $x$ のパラメーター $z = \theta^T x$ を代入します。
$$
{
h_\theta (x) = \frac{1}{1 + e^{-\theta^{\mathrm{T}} x}}
}
$$
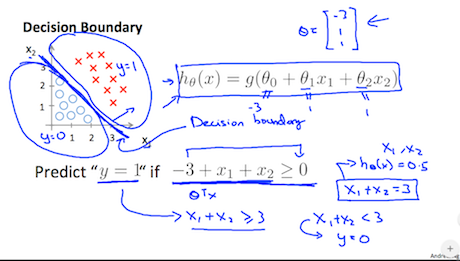
画像引用: Machine Learning - Coursera
$h_\theta(x)>0.5$ なら $y=1$
$h_\theta(x)\leq 0.5$ なら $y=0$
この様に分類判定が行えます。
ロジスティック回帰の目的関数と最急降下法
ロジスティック回帰の目的関数を求める時、対数 $log$ を利用します。
$y=1$ なら ${J(\theta) = -log(h_\theta (x)) }$
$y=0$ なら ${J(\theta) = -log(1 - h_\theta (x))}$
これをまとめると目的関数は以下の様になります。
$${ J(\theta) = - \frac{1}{m} [ \sum_{i=1}^m y^{(i)} log(h_\theta (x^{(i)})) + (1 - y^{(i)}) log(1 - h_\theta (x^{(i)}))] }$$目的関数を最急降下法に代入すると以下の様になります。
$${ \theta_j : \theta_j - \alpha \sum_{i=1}^m (h_\theta (x^{(i)}) - y^{(i)}) x_j ^{(i)} }$$基本式は単回帰・重回帰の時と同様です。
ロジスティック回帰の多クラス分類
応用変数 $y$ を複数設定する事で多クラス分類(Multiclass Classification)する事が出来ます。
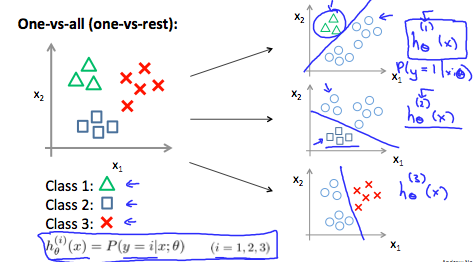
画像引用: Machine Learning - Coursera
One-vs-all という手法を使います。図をみるとわかり易いのですが、多クラスを仮の2クラスに分割して分類する手法です。
目的変数はどの様になるのでしょうか?
応用変数 $y_1$, $y_2$, $y_3$
に対し、目的変数はカテゴリーと同数のモデルが出来ます。
$$
{
h_\theta ^{(i)} (x) = P (y = i | x; \theta)
}
$$
それぞれのモデルは以上の様に表す事が出来ます。新たな $x$ が与えられた時、 $h_\theta ^{(i)} (x) $ が最大になるカテゴリーに分類されます。
では。