正則化 (Regularization)についてまとめてみます。
多項式回帰 (Polynomial Regression)
予測変数 $x$ 一つを元にして応用変数 $y$ を説明する場合、単回帰を利用します。
予測変数 $x$ が複数ある場合は重回帰となります。
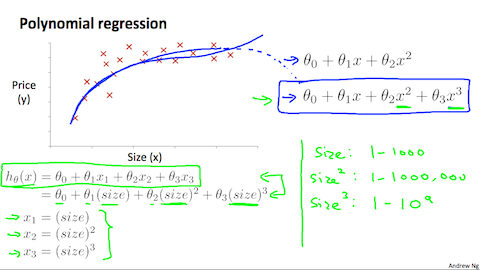
$x$ のパラメータ $\theta$ が複数ある回帰分析を多項式分析(Polynomial Regression)と呼びます。
予測する為のデータである $x$ を複数設定するのは分かるのですが、パラメータ $\theta$ を複数持つとどんな良い事があるのでしょうか?
画像引用: Machine Learning - Coursera
仮説関数は必ずしも直線を利用しなくても良いという事です。図の様にパラメータを複数設定する事でよりデータにフィットさせる事が可能になります。
オーバーフィッティング
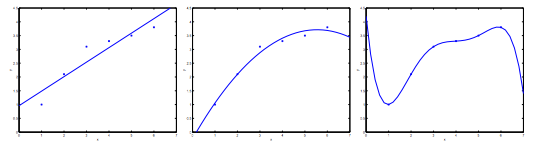
画像引用: Machine Learning - Coursera
多項式を使う事でよりデータにフィットした目的関数を得る事が出来ますが、オーバーフィッティング(過学習)した状態になると新しいデータに対して正しく推測する事が出来ません。
その対応として2つ方法があります。
- 特徴選択の数を減らす。(モデル選択のアルゴリズムを使う)
- 正則化する。(特徴選択の数は減らさずパラメータの値を小さくする)
正則化 (Regularization)
特徴選択の数を減らさずパラメータの値を小さくする事でよりスムーズに仮説関数を表す事が出来ます。
$${ J(\theta) = \frac{1}{2m} [ \sum_{i=1}^m (h_\theta (x^{(i)}) - y^{(i)})^2 + \lambda \sum_{j=1}^n \theta_j^2] }$$一つ目の $\sum$ (ループ)で二乗誤差法を用いて全ての点の誤差が最小であるパラメータ $\theta$ を求めます。
これだけ見るとかなり難しく感じるので、正則化パラメーター $\lambda$ (ラムダ)の中身をみてみます。
$${ \lambda \sum_{j=1}^n \theta_j^2 }$$別の$\sum$ (ループ)を使いパラメータ $\theta$ が膨張するのを妨げます。
この式のポイントは、以下の通り。
2つ目の $\sum$ の項が目的関数 $J(\theta)$ に入ることにより、$\theta$ の値を大きく取ると目的関数が最小値に近づけないように設計しています。
引用:Coursera Machine Learning (3): ロジスティック回帰、正則化 - Qiita
なるほど。パラメーターが大きすぎると、目的関数が0に近づかない様に設計されているという事です。ここで正則化パラメーター $\lambda$ (ラムダ)が生きてきます。
$\lambda$ (ラムダ)を大きくする事でより正則化が行えますが、あまりに大きすぎると $\theta_1$ 以降のパラメータが0の近似値となり、特徴量が失われてしまいます。
$\lambda$ (ラムダ)によりオーバーフィッティング、アンダーフィッティングを調整し、適正な正則化が行えるという訳です。
正則化はロジスティック回帰でも行えますが、ここでは省略します。では。