強化学習やってみました。ポンダッドです。

画像認識などの「教師あり学習」を試してみて、深層学習によって高精度の学習が可能だということはわかったのですが、今ひとつ想像していた「人工知能」とは違う印象を持ちました。

生物は経験をもとに学習していきます。上手くいけば喜び、上手くいかなければ悔しがったり、悩んだり…。そんなことの繰り返しの中で物事を覚え、上達していきます。

経験をもとにして学習する「教師なし学習」の一つとして「強化学習」という手法が以前より研究されています。これはどうも「大脳基底核」と呼ばれる脳の部位による活動を摸して機械に学習させる試みの様です。

自分の様な一般人が考える「人工知能」はこちらの方が近い気がします。

しかしながら、ちょっと考えただけでは簡単に理解することはできません。どうやって正解ラベルの無い環境から自ら学習することが出来るのでしょうか？

Q学習とは

強化学習における一つの手法として、Q学習というものがあります。ゼロからDeepまで学ぶ強化学習 - Qiita こちらの記事で分かりやすくまとめられていますので引用します。

Q-learningでは環境(モデル)の情報がない中でどうやって学習をするのでしょうか。その答えは「まず試してみる」となります。(中略) この「試行」を繰り返すことで学習していくわけです。

「『試行』を繰り返すことで学習していく」コンパクトにまとめられています。ここでいう「学習」とはQ値と呼ばれる「将来どれぐらいの報酬が期待できるか」という値を最大にする為どう行動すれば良いか？ということを指します。

Pythonで動作するサンプルコードを探してみたところ、以下のサイト

Q学習で最良経路をPythonで求めてみる - The jonki

で分かり易いPythonのサンプルコードを公開してくれていました。

jojonki/reinforcement-practice - GitHub

jonki　さんのコードをPython3系で動作する様に一部改変しました。

PonDad/simple3-q-learning.py - Gist

最良経路を求めてみる

以下のサイトの例題をPythonで解いていくという流れです。

A Painless Q-Learning Tutorial

リンク切れの際は、下記の中国語訳サイトをご参照下さい。

A Painless Q-learning Tutorial (一个 Q-learning 算法的简明教程)

以下の様な0〜5の6つの部屋を仮定して、ランダムなスタート位置からゴールである「部屋:5」に向かう最短経路を学習させます。

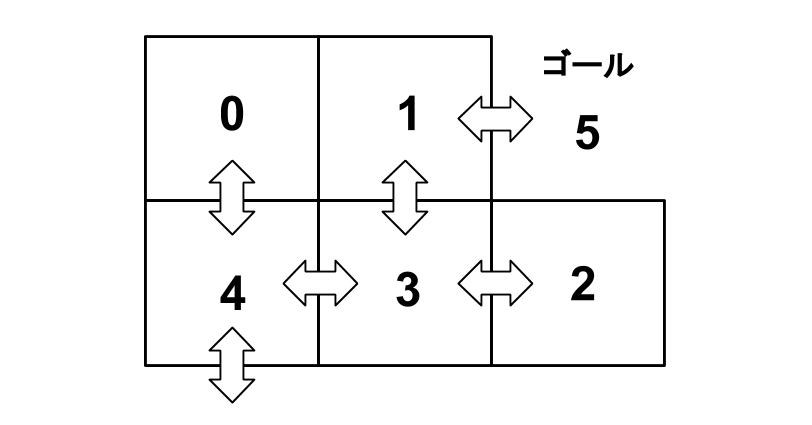
さて、まずはサンプルコードを実行してみます。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
$ python simple-q-learning.py
[[  0   0   0   0 359   0]
 [  0   0   0 287   0 449]
 [  0   0   0 287   0   0]
 [  0 359 230   0 359   0]
 [287   0   0 287   0 449]
 [  0 359   0   0 359 436]]
===== スタート =====
現在の部屋: 0
-> 行動: 4 に向かう
現在の部屋: 4
-> 行動: 5 に向かう
部屋: 5, ゴール!!
===== スタート =====
現在の部屋: 1
-> 行動: 5 に向かう
部屋: 5, ゴール!!
===== スタート =====
現在の部屋: 2
-> 行動: 3 に向かう
現在の部屋: 3
-> 行動: 1 に向かう
現在の部屋: 1
-> 行動: 5 に向かう
部屋: 5, ゴール!!
===== スタート =====
現在の部屋: 3
-> 行動: 1 に向かう
現在の部屋: 1
-> 行動: 5 に向かう
部屋: 5, ゴール!!
===== スタート =====
現在の部屋: 4
-> 行動: 5 に向かう
部屋: 5, ゴール!!

実行後、最初に表示されている配列は「Q値」を示しています。行が「部屋」を表し、列が「行動」を表しています。

例えば、「部屋:3」（配列の4行目）がスタートだとすると、「部屋:1」か「部屋:4」に向かうの「行動」の「Q値」が高くなっているのが分かります。移動可能な「部屋:2」へ向かうとゴールから遠ざかるので「Q値」が低くなっています。

その後のテストにより、どの部屋からスタートしてもゴールに最短距離で到達しているのが分かります。

さて、これはどんな仕組みになっているのでしょうか。

Q学習の仕組み

報酬

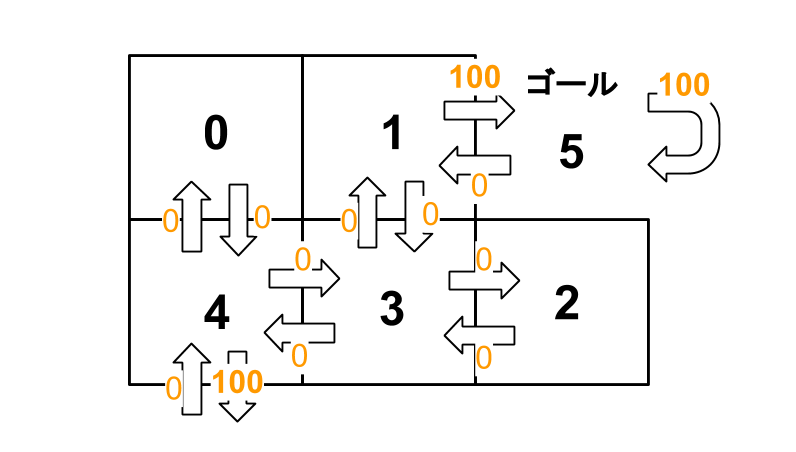
まず、ゴールに向かう「行動」に対し、「報酬」を設定します。

1
2
3
4
5
6
7
8
9
10
R = np.array([
[-1, -1, -1, -1,  0,  -1],
[-1, -1, -1,  0, -1, 100],
[-1, -1, -1,  0, -1,  -1],
[-1,  0,  0, -1,  0,  -1],
[ 0, -1, -1,  0, -1, 100],
[-1,  0, -1, -1,  0, 100]
])
GOAL_STATE = 5

移動不可能な「行動」に関しては-1とし、移動可能な「行動」を0にしています。ここではゴールの「報酬」を100としています。

割引率

1
GAMMA = 0.8

最短経路を学習するに当たって、先の報酬に対して割引をします。

Q値を最大化する

ここから「『Q値』を最大にする為どう『行動』すれば良いか？」を学習していきます。

1
Q = np.zeros((6,6))

Q値は初期化された状態から学習を開始します。

1
2
3
4
5
6
7
//実行結果
[[ 0.  0.  0.  0.  0.  0.]
 [ 0.  0.  0.  0.  0.  0.]
 [ 0.  0.  0.  0.  0.  0.]
 [ 0.  0.  0.  0.  0.  0.]
 [ 0.  0.  0.  0.  0.  0.]
 [ 0.  0.  0.  0.  0.  0.]]

「Q値」表す式はここではこの様に表せます。

Q(部屋, 行動) = 報酬(部屋, 行動) + 割引率 * 最大値[Q(次の部屋, 全ての行動)]

Q学習の基本式から一部簡略化されている部分はありますが、この式を利用して「『Q値』を最大にする『行動』」を求める事が出来ます。

試しに「部屋:2」からゴールに向かってみることにします。

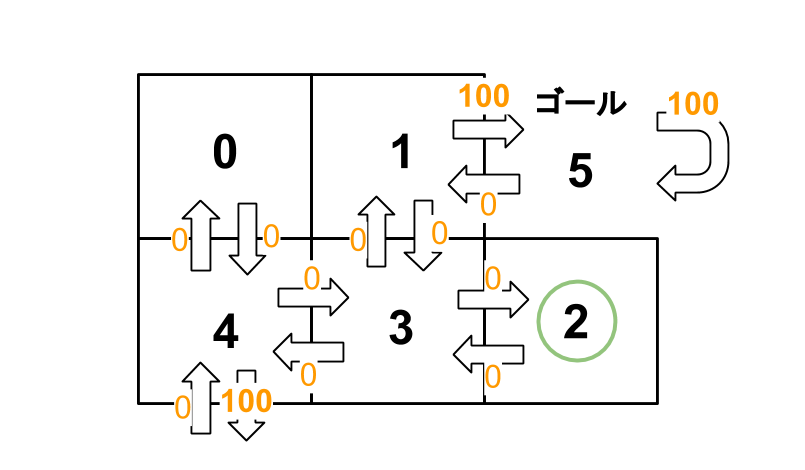
以下の経路でゴールしたとします。

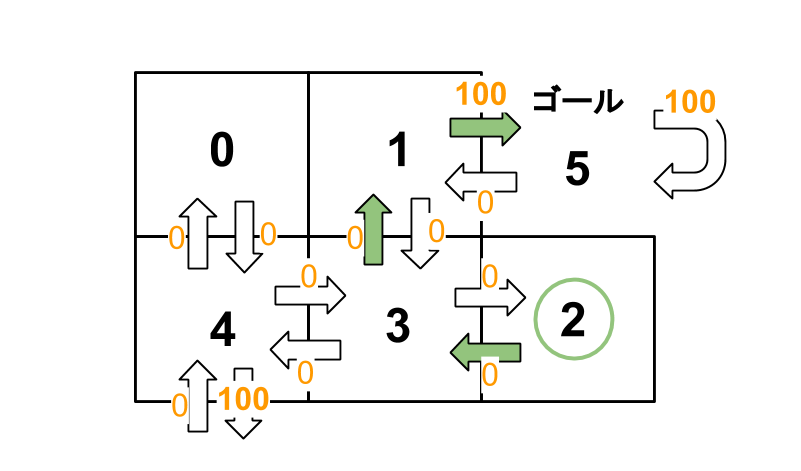
ゴールの「部屋:5」から移動可能な部屋は3つ、「部屋:1」「部屋:4」「部屋:5」です。

「部屋:1」から「部屋:5」に向かうQ値を数式に当てはめてみます。

Q(1, 5) = R(1, 5) + 0.8 * Max[Q(5, 1), Q(5, 4), Q(5, 5)] = 100 + 0.8 * 0 = 100

1
2
3
4
5
6
7
//実行結果
[[ 0.  0.  0.  0.  0.  0.]
 [ 0.  0.  0.  0.  0.  100.]
 [ 0.  0.  0.  0.  0.  0.]
 [ 0.  0.  0.  0.  0.  0.]
 [ 0.  0.  0.  0.  0.  0.]
 [ 0.  0.  0.  0.  0.  0.]]

「部屋:1」から「部屋:5」に向かうQ値は100になりました。

「部屋:1」から移動可能な部屋は「部屋:3」と「部屋:5」です。

「部屋:3」から「部屋:1」への移動を数式に当てはめてみます。

Q(3, 1) = R(3, 1) + 0.8 * Max[Q(1, 3), Q(1, 5)] = 0 + 0.8 * Max[0, 100] = 80

1
2
3
4
5
6
7
//実行結果
[[ 0.  0.  0.  0.  0.  0.]
 [ 0.  0.  0.  0.  0.  100.]
 [ 0.  0.  0.  0.  0.  0.]
 [ 0.  80.  0.  0.  0.  0.]
 [ 0.  0.  0.  0.  0.  0.]
 [ 0.  0.  0.  0.  0.  0.]]

「部屋:3」から「部屋:1」に向かうQ値は80になりました。

この様にしてランダムに部屋を抽出し、1000回学習させます。

1
2
import random
LEARNING_COUNT = 1000
1
2
3
4
5
6
7
//最終的な実行結果
[[  0   0   0   0 371   0]
 [  0   0   0 296   0 463]
 [  0   0   0 296   0   0]
 [  0 371 237   0 371   0]
 [296   0   0 296   0 463]
 [  0 363   0   0 371 454]]

最終的な結果はこの様になります。こうして「『Q値』を最大にする『行動』」を求める事が出来ました。

ε-グリーディ法

「最良の経路を選択する。」と言ってもそのケースによって異なります。目先の最短の経路を選択するよりも、一見遠回りに見えても長期的に見れば報酬が高くなるケースもあるからです。

ここではε-グリーディ法に沿って言えばε=0とし、探索はせずに一番高い報酬が期待出来る行動をとります。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
//実行結果
===== スタート =====
現在の部屋: 0
-> 行動: 4 に向かう
現在の部屋: 4
-> 行動: 5 に向かう
部屋: 5, ゴール!!
===== スタート =====
現在の部屋: 1
-> 行動: 5 に向かう
部屋: 5, ゴール!!
===== スタート =====
現在の部屋: 2
-> 行動: 3 に向かう
現在の部屋: 3
-> 行動: 1 に向かう
現在の部屋: 1
-> 行動: 5 に向かう
部屋: 5, ゴール!!
===== スタート =====
現在の部屋: 3
-> 行動: 1 に向かう
現在の部屋: 1
-> 行動: 5 に向かう
部屋: 5, ゴール!!
===== スタート =====
現在の部屋: 4
-> 行動: 5 に向かう
部屋: 5, ゴール!!

この様に行動します。

まとめ

正解ラベルの無い環境から自ら学習出来ることが出来る事が分かりました。ディープラーニングと組み合わせる事で、更に複雑な計算も高速に行える様になっている様なので試してみたいですね。

ではまた。

参考書籍

イラストで学ぶ　人工知能概論 (ＫＳ情報科学専門書) Kindle版 - Amazon.co.jp