『階層的一時記憶』を紐解く〜HTM/Hierarchical temporal memory
2045年まであと15年。こんにちは、ポンダッドです。
数回にわたってまとめてきたジェフ・ホーキンスの理論により、知能の未来が見えたように感じました。
「脳をリバース・エンジニアリング」した「機械知能」と聞くと、スーパーコンピューターでも使うのかと想像しますが、64ビットのパソコンと公開されているプラットフォームで誰でも使うことができます。
今回は機械知能の奥底へ潜り込み、その理論にせまります。みなさんも電脳世界へダイブしてみましょう。
階層的一時記憶(HTM/Hierarchical temporal memory)
ホーキンスが『考える脳考えるコンピューター』執筆した後、構築したシステムは階層的一時記憶(以下HTM)と名付けられました。
今回考察するのは、第二世代アルゴリズムになります。主にNumenta社の公開している情報※1を参照します。
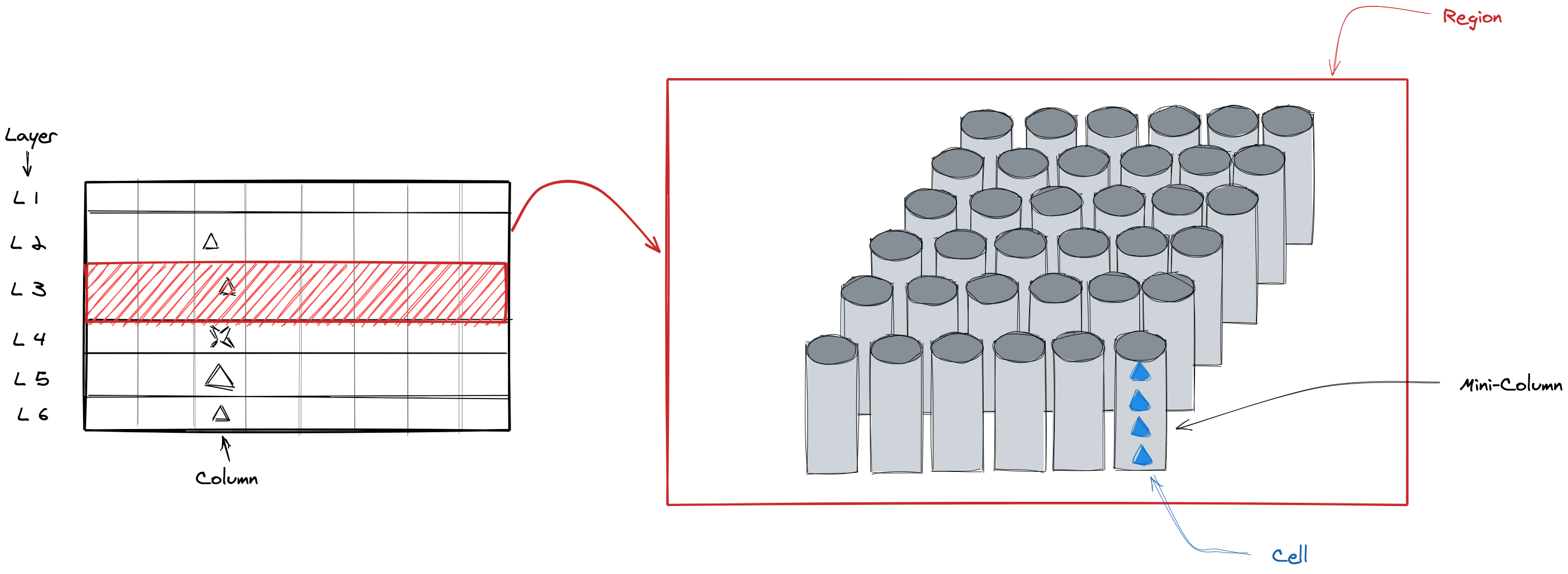
図1:HTM概念図
HTMは、新皮質の領域(リージョン/Region)の構造をもとにしています。旧脳は含まれず、脳全体を再現したものでないことに注意してください。
新皮質はどの領域でも均一にはたらきますので(マウントキャッスルの発見)、ひとつの領域は「記憶による予測」をおこなう最小単位として機能します。
HTMのリージョン(Region)は新皮質の柱状構造を模しており、ミニカラム(Mini-Column)の集合(Mini-Columns)からできています。ミニカラムは複数のセル(Cell)をもちます。
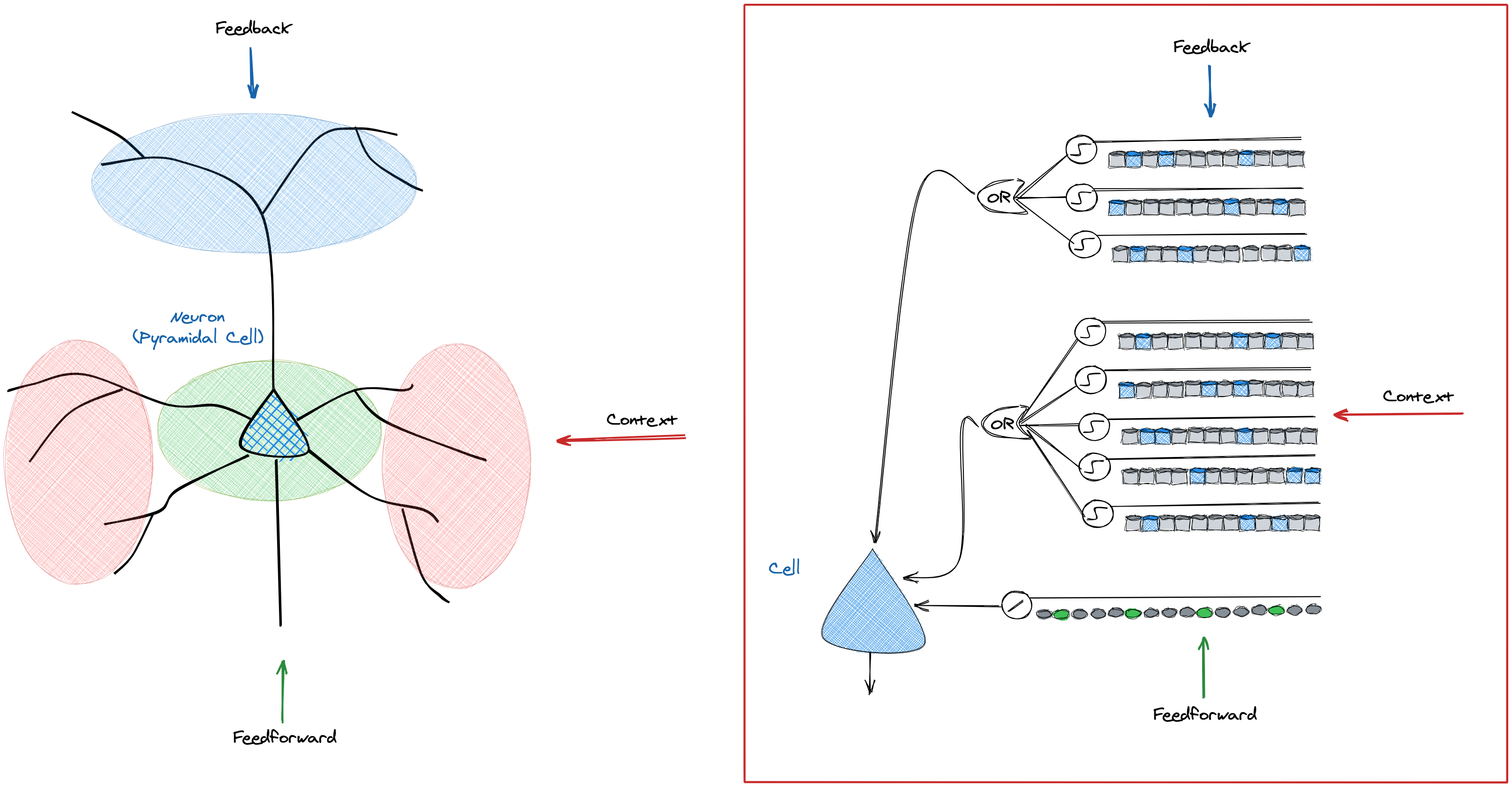
図2:HTMにおけるセルの機能
HTMのセルは、新皮質の錐体細胞の機能を再現します。「入力データ」をフィードフォワード(Feedfoward)「普遍の表現」をフィードバック(Feedback)として受け取ります。
入力データは視床を通じて第1層に戻り、領域全体に広がります。それをもとに新皮質は「自己連想記憶」を呼び出しました。HTMセルは、シナプスの結合状態から「文脈」(Context)をとらえ、「自己連想記憶」を呼び出します。
スパース分散表現(SDR/Sparse Distributed Representations)
HTMでは情報をスパース分散表現(SDR)で表現します。これは、新皮質のニューロンがまばらに活性化されることにヒントを得ました。
SDRでは記憶をバイナリデータ※2で表現します。「アクティブ」と判断されたものはオンビット1で表現され、「非アクティブ」と判断されたものはオフビット0で表現されます。オンビットはSDRの2%ほどで設定され、オフビットは98%の疎状態(Sparsity/スパース状態)になります。

図3:スパース分散表現
SDRが疎状態であることから得られる特性は以下のようになります。
- 1兆を超える(240)容量を持ち※3、ミスマッチの発生確率が低い
- 疎状態であるため堅牢性が高く、ノイズによる誤差確率が低い
- 疎状態のベクトルを処理するため、分類エラー率が低い※4
- SDRは結合(ユニオン/Union)※5できるため、複数同時の予測が可能になる
- ノイズが存在する場合でも、SDRユニオンは堅牢性が高い
一般的なニューラル・ネットワークは、密な情報である特徴量を細かく学習します。スパース分散表現はその真逆の発想であることが分かります。
エンコード(Encode)
さまざまな入力データを、SDRにエンコードすることで新皮質と同じ処理が可能になります。HTMシステムでは、エンコード用のAPIが用意されています。いくつか例をあげます。
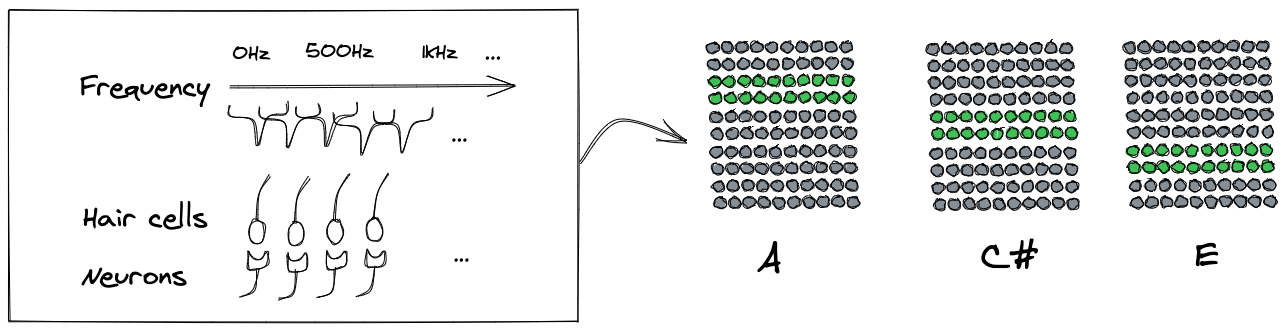
図4: 周波数のエンコード
もっとも一般的な入力データは数値といえます。たとえば、音階周波数ごとに入力データをSDRに変換することで、HTMで音階の学習、予測がおこなえます。
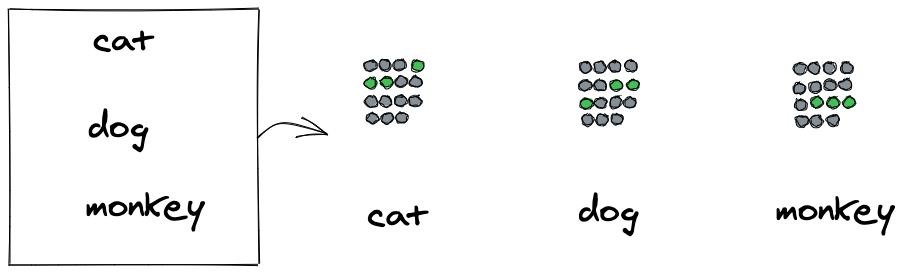
図5: 分類のエンコード
数値データを伴わない場合、値の変化から意味を表現できます。
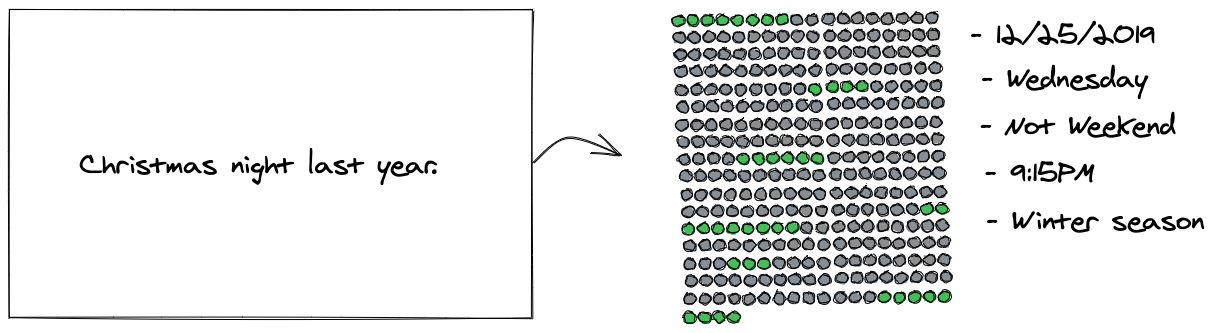
図6: 日時のエンコード
複数の意味空間を含んだ入力データをエンコードできるAPIも用意されています。汎用性のたかい日時に関しては細かい条件でエンコードが可能です。
空間プーリング(SP/Spatial Pooling)
HTMの入力に対する学習と推論※6は、空間プーリング(Spatial Pooling)と呼ばれるアルゴリズムによっておこなわれます。
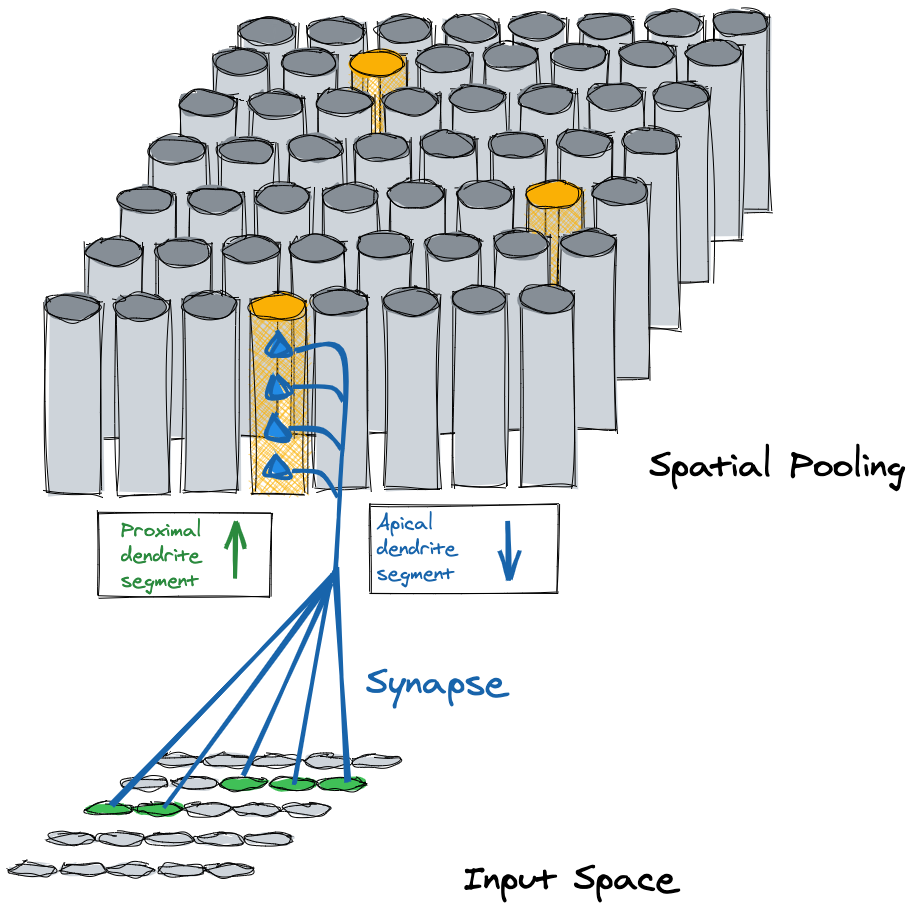
図7: 空間プーリング
空間プーリングを実行するHTMリージョンを空間プーラーと呼びます。図7の例でいうとデータ構造はSDRを4枚重ねたもので表すことができます。空間プーリングは、入力データとミニカラム間のフィードフォワード接続を学習します。
空間プーラー内のミニカラムにあるセルは、樹状突起(じゅじょうとっき/Dendrite)セグメント(Segment)を通じ、シナプス(Synapse)によって入力データと接続します。
シナプスは入力データと空間プーラーの情報を比較し、その結合度によって抑制をおこないます。抑制の結合度を示すしきい値は初期値ではランダムに設定されます。(図2ではステップ関数で示されています)
また、シナプスは入力データを、より多く空間プーラーに接続しようとします。これをブースティング(Boosting)とよびます。接続するシナプスの数は、任意のミニカラムが隣接するミニカラムに対してアクティブになる頻度によって決まります。(図2では一次関数で示されています)
ブースティング後、抑制値が高いミニカラムはアクティブな状態を保ち、それ以外のミニカラムは非アクティブな状態となります。
アクティブなミニカラムに接続したシナプスは永続値(parmanence)が上昇し、非アクティブなミニカラムに接続したシナプスは永続値が減少します。これにより接続から非接続に、その逆に変更されます。
まとめると空間プーリングは、入力データとミニカラム間の永続値を学習し、接続状態を更新します。
一時記憶(TM/Temporal Memory)
HTMのシーケンス学習と入力に対する予測は、一時記憶(Temporal Memory)アルゴリズムによっておこなわれます。
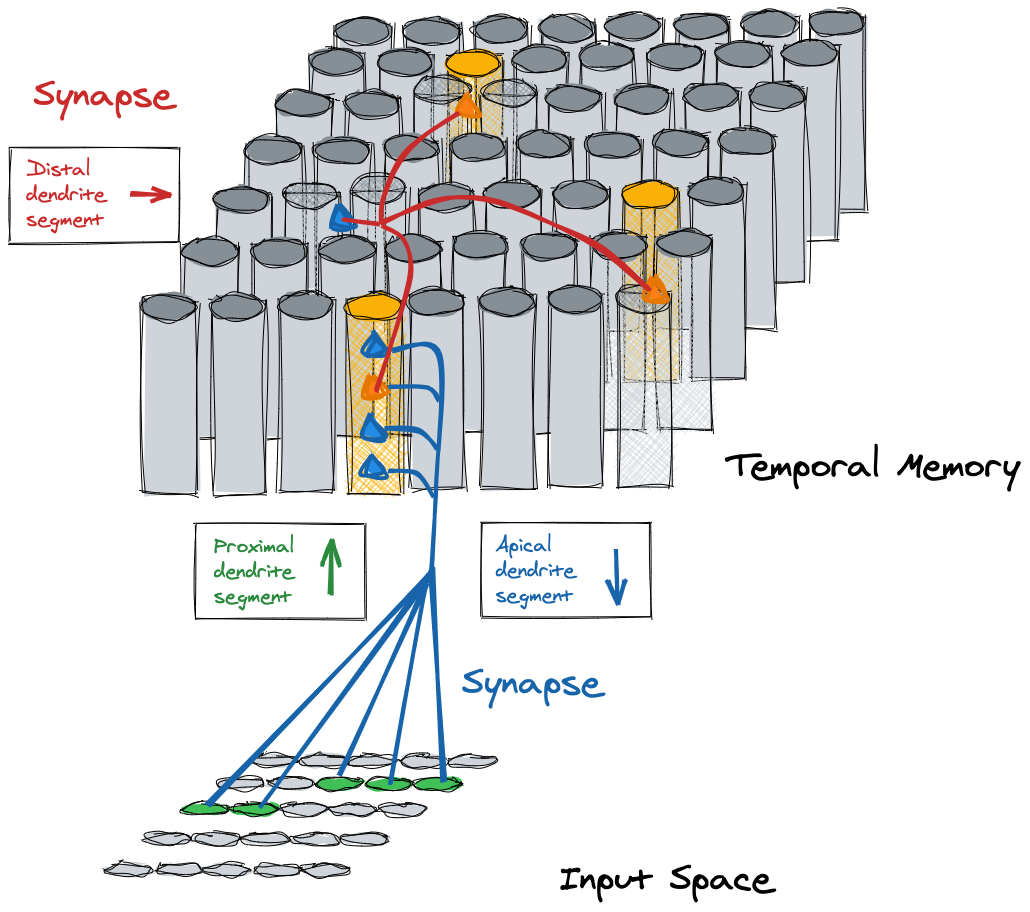
図8:一時記憶
一時記憶を実行するHTMリージョンを時間プーラーと呼びます。空間プーラーと同様、図8の例でいうとデータ構造はSDRを4枚重ねたもので表すことができます。時間プーラーは同じリージョンのセル間の接続を学習します。
時間プーラー内のセルは、樹状突起セグメントを通じ、シナプスによってその他のセルと接続します。
一時記憶は学習後、2つのステップに分かれてアルゴリズムを実行します。
学習時、ミニカラムがはじめてのデータを参照する際、それらは予測にないためバースト(Burst)が発生します。つまり、ミニカラムのすべてのセルがそのシーケンスを学習しようとします。
学習後、ひとつめのステップが実行されます。バーストしたミニカラムでは、特定のセルのみがアクティブになります。
ふたつめのステップでは、特定のセルがアクティブになったと識別されると、次に発火する複数のセルが予測されます。
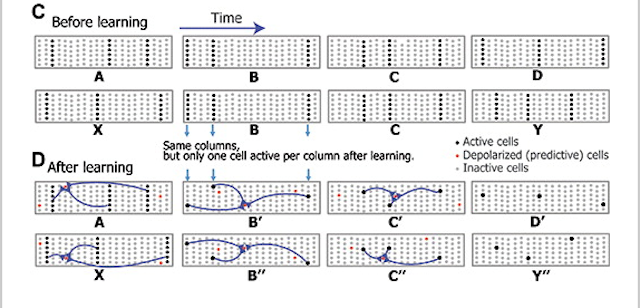
図8: 一次記憶の学習前、学習後 (引用: The MIT Pless Jpuenals)
論文の図をみると分かりやすいので引用します。A→B→C→D→X→B→C→Yの順で学習したのち、Cを入力した時の予測をみてみましょう。
Cの入力時、一時記憶によってセルがシーケンスを学習しているため、Cの入力前がB’であればD’が予測されます。また、Cの入力前がB’’であればY’’が予測できます。
まとめると一時記憶は、HTMリージョンのセル間の接続の永続値を学習し、接続状態を更新します。そして、入力の次のシーケンスを予測します。
まとめ
第2世代アルゴリズムはオンラインで教師なし学習ができるため、異常検知などの分野での活用が見込まれています。
今回は機械知能の秘密にせまりました。はじめは難解に思えましたが、『考える脳考えるコンピューター』で論じられた脳の構造と照らし合わせると、理解が深まりました。
ホーキンスは「優れた理論とは簡単に理解されるものである」というモットーを持っているようです。ブラックボックス部分がないので、今後はひろく世の中に受け入れられるような気がします。
とくに根拠はないのですが。そう囁くのです、私の中のゴーストが。
来週はHTMを実際に使ってみます。次回「機械知能に歌おぼえさせてみた」おたのしみ!
引用/注釈
※1: 以下のアドレスで公開されている論文・動画・文献をGoogle/DeepLにて翻訳し、参考にしました。
Hawkins, J. et al. 2016-2020. Biological and Machine Intelligence. Release 0.4. Accessed athttps://numenta.com/resources/biological-and-machine-intelligence/.
※2: バイナリ(wikipedia)
※3: SDRがデフォルト値の場合。2048ビットの2%で40ビットになり容量は240になります。
※4: 疎状態と密状態の比較は、補足図のBとCを参照してください。
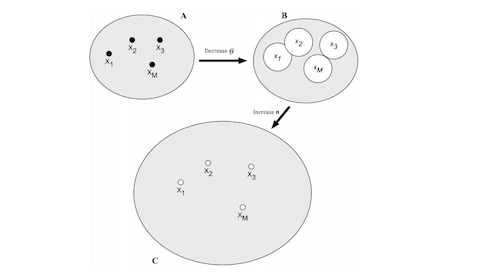
補足図: 疎状態と密状態の比較
※5: SDRユニオンはOR演算をおこないます。その際、一種の正則化おこないスパース値を2%で保ちます。
※6: シーケンスを伴わないものは、予測ではなく「推論」としました。