深層学習やってみる - ニューラル・ネットワークの仕組みを考える

明けましておめでとうございます。ポンダッドです。

深層学習用のライブラリと学習済みモデルを使って、機械が学習出来ることは分かったのですが、一つ疑問に思うことがあります。

「機械が自分で『学習する』ってどういうことなんだろうか？」

今回はその仕組みをちょっと考えてみることにします。

人工知能に関する断創録さんの記事を参考にしながら進めてみたいと思います。

ニューラル・ネットワークの仕組み

上記のブログ記事の中で、kerasの手順をこの様にまとめていました。

データのロード
モデルの定義
モデルのコンパイル
モデルの学習
モデルの評価
新データに対する予測

1,5,6の項目に関しては、通常の機械学習の流れと同じなので、どうも2,3,4の部分に秘密がありそうです。

さて、今回はお手本のブログと同様、UCI Machine Learning repositoryの
Pima Indians Diabetes Data Set を利用します。これはPimaインディアンが8つの医学的な情報を元に糖尿病に掛かったか否かを示すデータです。

2つのクラスに分類するニューラルネットワークはKerasを使いこんな風に記述出来ます。

import os
import numpy as np
from keras.models import Sequential
from keras.layers import Dense
from keras.utils import np_utils
from keras.utils.visualize_util import plot
from sklearn.cross_validation import train_test_split
seed = 7
np.random.seed(seed)
if __name__ == "__main__":
    # 1.データのロード
    dataset = np.loadtxt(os.path.join("..", "data", "pima-indians-diabetes.data"), delimiter=',')
    X = dataset[:, 0:8]
    Y = dataset[:, 8]
    X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.3, random_state=0)
    # 2.モデルの定義
    model = Sequential()
    model.add(Dense(12, input_dim=8, init='uniform', activation='relu'))
    model.add(Dense(8, init='uniform', activation='relu'))
    model.add(Dense(1, init='uniform', activation='sigmoid'))
    # 3.モデルのコンパイル
    model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
    # 4.モデルの学習
    model.fit(X_train, Y_train, nb_epoch=150, batch_size=10)
    # 5.モデルの評価
    scores = model.evaluate(X_test, Y_test, verbose=0)
    print("%s: %.2f%%" % (model.metrics_names[1], scores[1] * 100))
    # 6.新データに対する予測
    predictions = np.round(model.predict(X_test))
    correct = Y_test[:, np.newaxis]
    print(predictions[0])
    print(correct[0])

モデルの学習

まずは流れを画像でみていきましょう。

Kerasをターミナルで実行すると、学習の進捗を確認することができます。

指定したepocの回数分（ここでは150回）繰り返し学習していることが分かります。学習を重ねる毎にloss（訓練データの損失）が下がり、acc（訓練データの精度）が上昇しているのが分かります。

グラフで出力してみてみましょう。

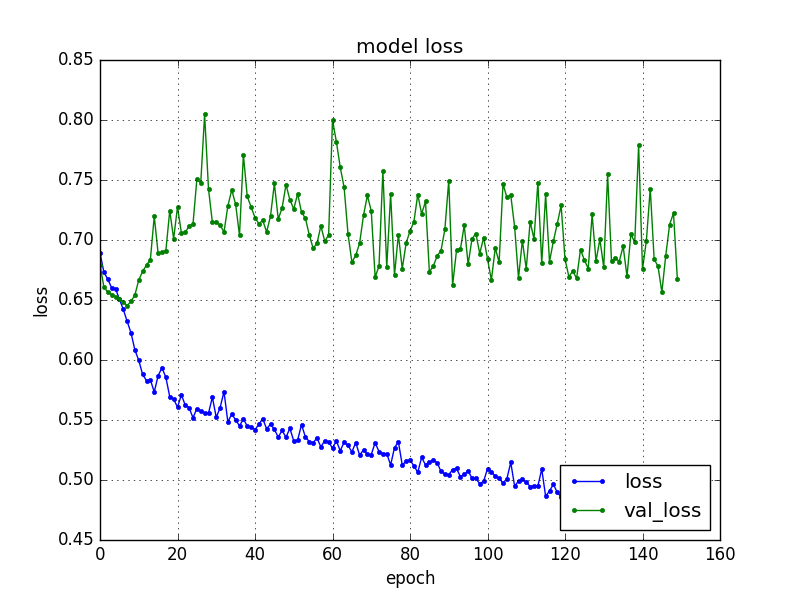
loss（訓練データの損失）が下がっていることが視覚的に分かります。ちょっと気になるのがval_loss（検証データの損失）は下がっていないことです。

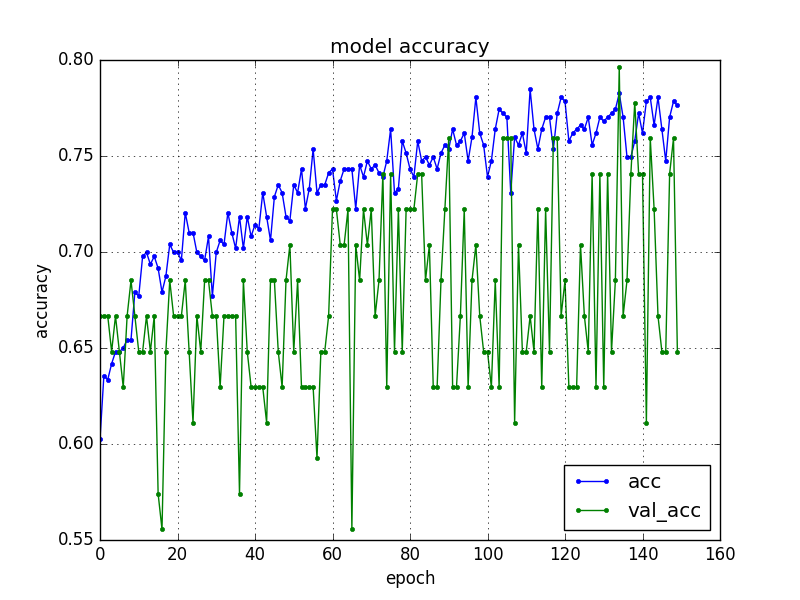
acc（訓練データの精度）は回数を重ねる毎にval_acc（検証データの精度）が上がっていることが分かります。

最後にacc: 73.59%と言う結果になりました。

※epocを1,000回にして試してみたところ、以下の様にval_lossが逆に上がってしました。これはどうやら過学習と呼ばれる状態の様です。

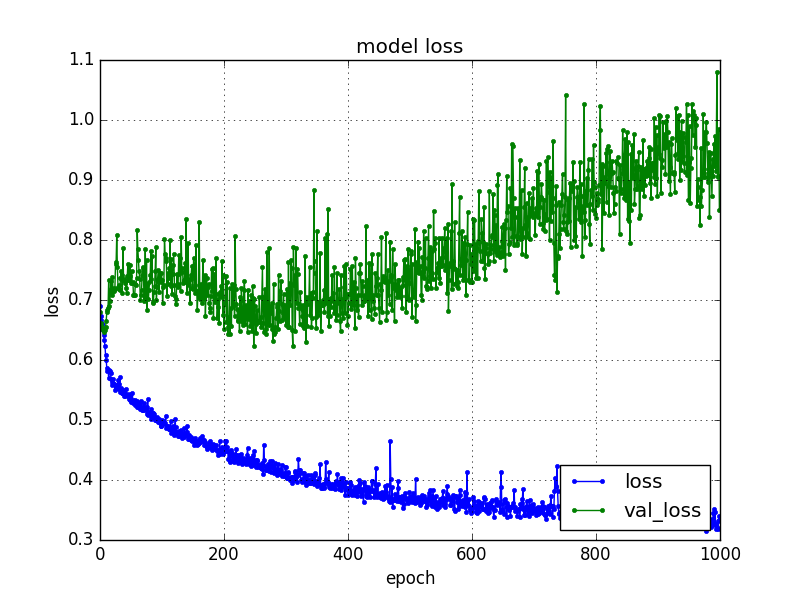
学習用の元になるデータを学習し過ぎて、肝心なデータを分析する為の特徴量が見えなくなってしまう。ということの様です。

機械が学習する。と言っても「教師あり学習」を行う際は、適正な学習方法をセットしなければならない様ですね。

この部分のプログラムはこの様になります。

1 2	# 4.モデルの学習 model.fit(X_train, Y_train, nb_epoch=150, batch_size=10)

メソッドnb_epochで学習回数を指定しています。batch_sizeは10となっています。バッジサイズとは何でしょうか。これは学習を効率的に行う指数の様です。（※ここではデータ10個分の誤差で1回重みを更新するという指定です）

ここで気になるのは、どうやって機械が損失を減らしているかと言うことです。

さて、もう一歩ニューラルネットワークの深淵に踏み込んでみることにしましょう。

モデルのコンパイル

コンパイルのプログラムはこの様になります。

1 2	# 3.モデルのコンパイル model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])

ここでは、損失関数loss、最適化関数optimizer、評価指標metricsを指定しています。

この部分がニューラル・ネットワークにおいては最も重要な部分の様です。

ニューラル・ネットワークは損失関数を元に損失を減らすことを目的とします。その為に「誤差逆伝播法」というアルゴリズムを利用します。

入力された重みは損失関数lossを元に傾斜（勾配というそうです）を計算し、誤差逆伝播法によってフィードバックされ、重みが更新される仕組みとなります。

それによって損失を下げていくという訳です。

最適化関数optimizerというものがメソッドとしてありますが、これを図で示すとこの様になります。

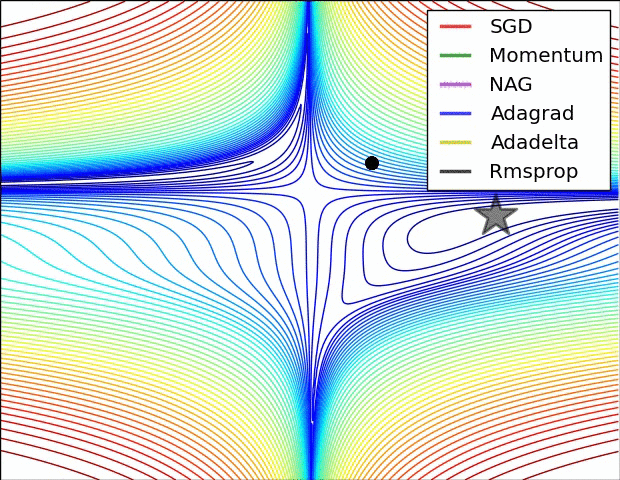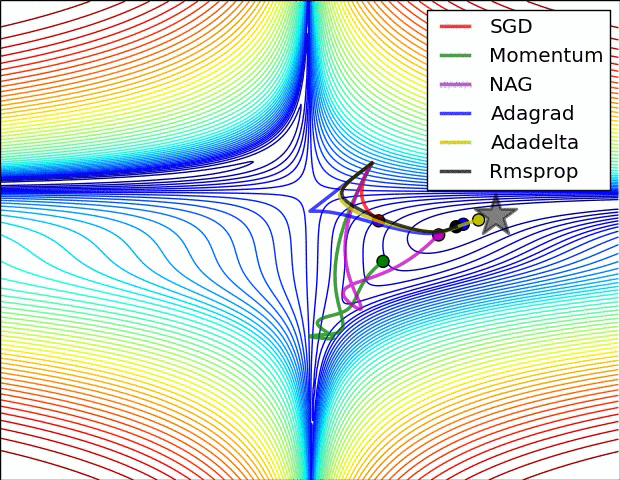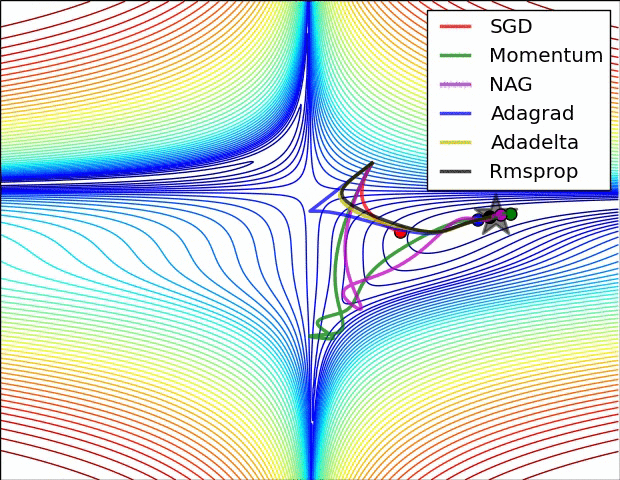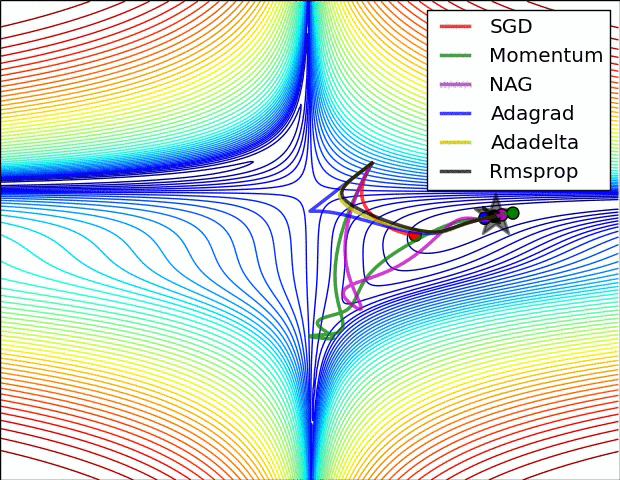
Visualizing Optimization Algos

なんか映画の異次元空間みたいな図ですが、これは損失曲線における確率的勾配降下法を示しています。

ここではこの図の様に損失がアルゴリズムによって坂道（勾配）を下ることをイメージ出来れば良いのではないかと思います。（今回はadamという最適化アルゴリズムを利用しています。）

モデルの定義

さて、ニューラルネットワークは何層にも渡り元となるデータにフィルターを掛けることで特徴量をより明確にしていきます。

プログラムはこの様になります。

# 2.モデルの定義
model = Sequential()
model.add(Dense(12, input_dim=8, init='uniform', activation='relu'))
model.add(Dense(8, init='uniform', activation='relu'))
model.add(Dense(1, init='uniform', activation='sigmoid'))

今回は元となるデータが8次元です。

# 訓練データ
X_train[0] = [6,148,72,35,0,33.6,0.627,50]
# 訓練ラベル
Y_train[0] = [1]

その為、入力層は8次元となります。入力層8次元→隠れ層12次元→隠れ層8次元→出力層1次元となり、図で表すとこんな感じです。

実際はパーセプトロン同士がお互いシナプスで繋がって、お互いに結び付いています。層ごとに活性化関数activationを設定します。

relu関数はこの様な関数です。

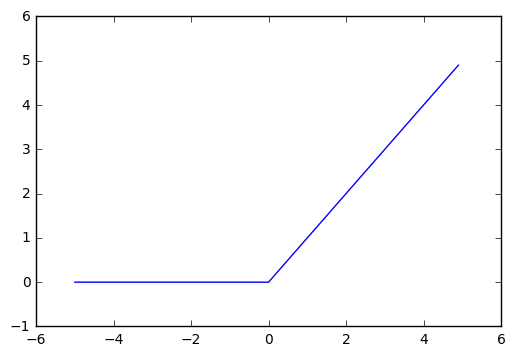
一見単純な関数に見えますが、隠れ層にはこのrelu関数を使うことで精度が高まるそうです。

sigmoid関数はこんな関数です。

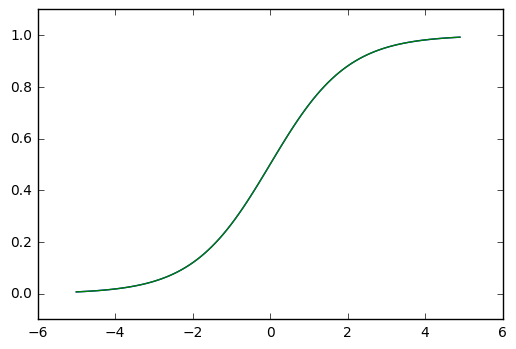
sigmoid関数を使うと0.0から1.0の値が出力されます。その為今回の場合は0.5を閾（しきい）値として2クラス分類することが出来ます。

多クラス分類の場合はsoftmax関数を利用し、0.0から1.0の正規化されたデータを元に分類するケースが多い様です。

乱数発生の初期化

本文では触れませんでしたが、プログラムの冒頭でNumpyを使って発生する乱数を初期化しています。

1 2	seed = 7 np.random.seed(seed)

この様に設定しておけば、毎回同じ乱数を発生させることが出来ます。ニューラルネットワークでは重さの初期化に乱数を利用するそうです。

1	model.add(Dense(12, input_dim=8, init='uniform', activation='relu'))

モデル構築する際のinitメソッドで定義します。機械が学習する為に乱数を用いるなんてちょっとロマンを感じますね。

まとめ

ニューラルネットワークの仕組みを図を使ってまとめてみることで、ブラックボックス的に感じていた深層学習方法が少し頭の中でイメージしやすくなりました。

最近聞きかじった知識を元にざっくりまとめたものですので、正確でないものがあるかもしれませんので、そこは予めご容赦下さい。

さて、今回は8次元のデータを2つのクラスに分類するだけだったのですが、もっと複雑なデータ、例えばカラー写真データを取り扱うとなったらどうでしょうか。

299×299ピクセルのカラー画像を配列にしてみると、268,203次元もの配列になります。どうも単純に全結合したニューラルネットワークではその特徴量を十分に抽出できない様です。

そこで考え出されたのがCNN(コンボリューションニューラルネットワーク)です。

（つづく）