こんにちは、人工知能愛好家（Artificial Intelligence Hobbyist）ポンダッドです。英語で書くとなんかカッコイイですね。

さて、前回からの続きとなります。

ニューラル・ネットワークの仕組みが考え出されたのはのは1980年代のことの様ですが、その後衰退してしまったそうです。それは何故なのでしょうか。

全結合ニューラル・ネットワークの問題点

ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装 - Amazon.co.jpのp207より引用させて頂きます。

全結合の問題点は何でしょうか。それはデータ形状が”無視”されてしまうことです。例えば入力データが画像の場合、画像は通常、縦・横・チャンネル方向の３チャンネルです。しかし、全結合層に入力するときには、3次元データを平ら-1次元のデータ-にする必要があります。

例えばこのゾウさんの画像を元に考えてみます。

このカラー画像を299×299ピクセルのカラー画像（3チャンネル）をフラットにしてみると、268,203次元もの配列になります。

例えばこれら元に千種類に分類できるの1千万枚の画像を10層のニューラルネットワークで学習させてみると仮定します。

実際は入力部分が1千万枚分あります。約26兆個のニューロンを全てシナプスで繋げて、誤差逆伝播法に基づき例えば千回学習させてみるとしましょう。

ちょっと乙女座の聖闘士が使う様な単位が頭に浮かんでしまいました。そんな計算が当時そう簡単に行えるとは思えません。

そもそも、（以下再び引用）

画像は3次元の形状であり、この形状には大切な空間情報が含まれているでしょう。（略）しかし、全結合層は、形状を無視して全ての入力データを同等のニューロン（同じ次元のニューロン）として扱うので、形状に関する情報を生かすことができません。

フラットにしたデータではカラー画像の特徴量は抽出不可能な様です。

更に、学習効果を高める為、層を厚くすると「勾配消失」と言って、特徴量が限りなく0に近づいてしまうという問題があるそうです。

さて、そういった経緯で一旦ニューラルネットワークによる研究は長らく冬の時代に突入してしまった、ということの様です。

畳み込みニューラル・ネットワーク

さて、それでは近年盛んに言われる「深層学習」では、どの様にしてその問題を突破したのでしょうか。その解決となったのが「畳み込みニューラル・ネットワーク（CNN/コンボリューションニューラルネットワーク）」です。

この技術によってニューラル・ネットワークの層を重ねることが可能になり、人間を越える精度で物体認識が出来る様になりました。

上のゾウさんの画像を畳み込みニューラル・ネットワークで学習したモデルに見せると、「インド象87.6%、アフリカ象2.8%」と回答します。

まるで魔法の様ですが、今回は「畳み込みニューラル・ネットワーク」がどの様に行われているか、その中身をちょっとのぞいてみることにします。

深層学習ライブラリはなんと、JavaScriptを使って、ブラウザで動作させることも可能になっています。以下のサイトで実際にデモを試すことが出来ます。

Keras.js Demos

Googleの開発した高精度の学習モデルInceptionV3を使ったデモも試せます。こちらを使い、畳み込みニューラル・ネットワークがどの様に行われているかみていきましょう。

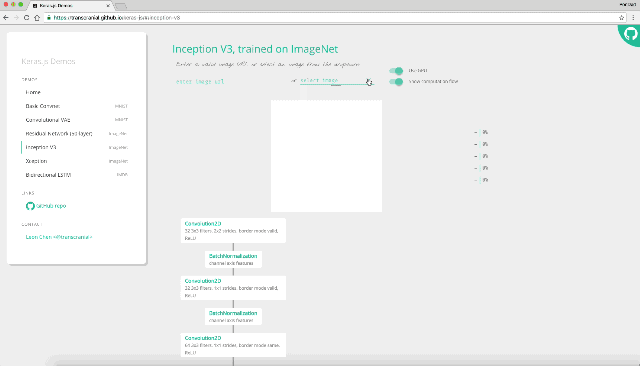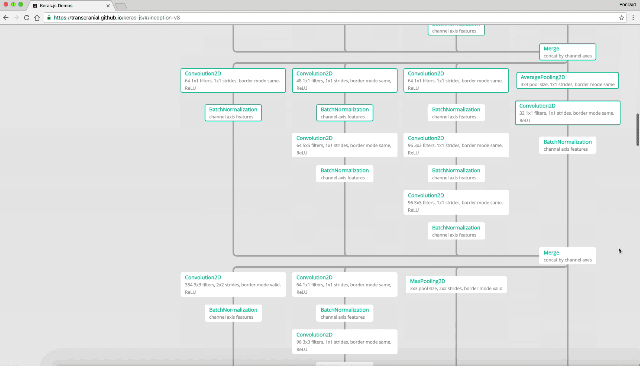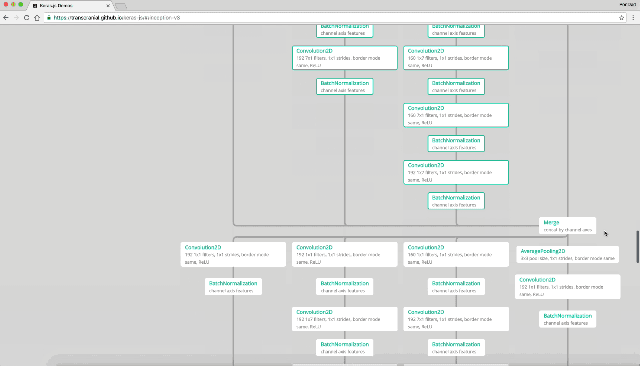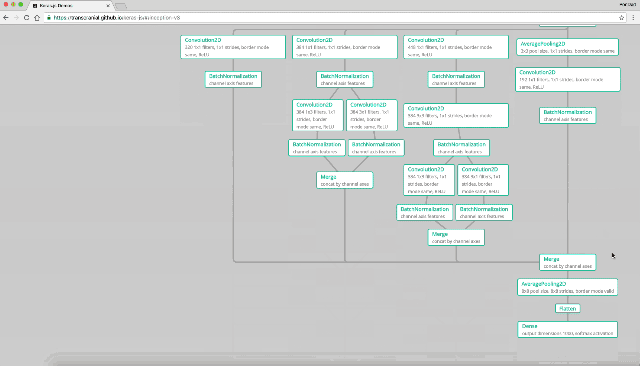
凄いですね。10層どころでは無い程深く層を重ねています。ここでは最後にきちんと「りんご」と判定しているので、全結合ニューラル・ネットワークでみられる勾配喪失の問題がクリアされているのが分かります。

それでは、ここでは何が行われているのでしょうか。深層学習の深淵をちょっと覗いてみることにします。

何層にも重ねられたニューラル・ネットワークですが、良くみると同じ様な処理を繰り返しているのが分かります。全結合ではみられなかった処理が行われれいる様です。

では最初の部分を切り出してみます。

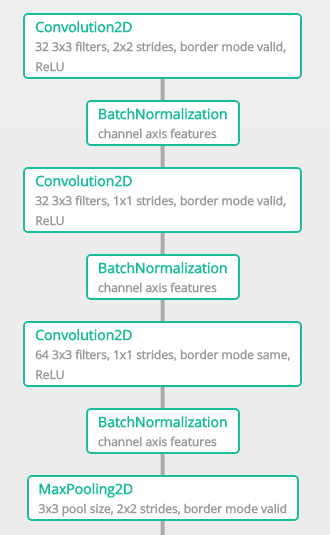
どうも、Convolution2D→BachNormalizationを繰り返し最後にMaxPooling2Dという処理を行なっている様です。

基本的には同様の処理を繰り返し行なっています。

kerasのサンプルプログラムも合わせて覗いてみます。

1
2
3
4
x = conv2d_bn(img_input, 32, 3, 3, subsample=(2, 2), border_mode='valid')
x = conv2d_bn(x, 32, 3, 3, border_mode='valid')
x = conv2d_bn(x, 64, 3, 3)
x = MaxPooling2D((3, 3), strides=(2, 2))(x)

（当たり前ですが）デモと同様の記述がしてあります。

この「Convolution層」と「Pooling層」を繰り返し重ねることに畳み込みニューラル・ネットワークの秘密が隠されている様です。

さて、学習の最後はこの様になっています。

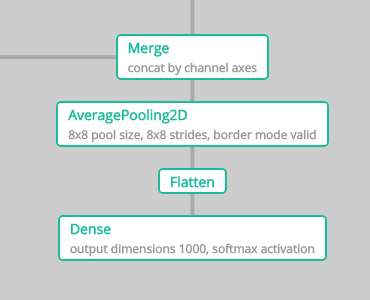
同じくサンプルプログラムを覗いてみます。

1
2
3
x = AveragePooling2D((8, 8), strides=(8, 8), name='avg_pool')(x)
x = Flatten(name='flatten')(x)
x = Dense(1000, activation='softmax', name='predictions')(x)

これは予想通り、flattenで3次元データを1次元に変換してフラットにした後、softmax関数を利用して1,000次元で出力しています。（ラベルが1000種類ある為）

ここで全結合ニューラル・ネットワークに戻る訳ですね。

ようやく「Convolution層」と「Pooling層」が畳み込みニューラル・ネットワークの鍵になることが分かりました。

さて、更なる深淵を覗き込んでみることにしましょうか。

(つづく)