久しぶりの更新です。実は「微分」って良く分からなかったのでこんな本を読んでみました。
マンガでわかる微分積分 微積ってなにをしているの?どうして教科書はわかりにくいの? (サイエンス・アイ新書)
イラストを利用した入門書で少し理解が進んだ(様な気がする)のでまとめたいと思います。
微分(differential)とは
「変化の分析」をするものであり、微分した結果というのは直線で言えば傾きとなります。
$$
y = f(x)
$$
という曲線グラフ上のaという1点の傾きは以下のように求められます。
$$
\lim_{h \to 0} \frac{f(a+h)-f(a)}{h}
$$
数式で見ると難しく感じますが、曲線上の1点aの 縦の長さの差÷横の長さの差の最小値を求めるという意味です。
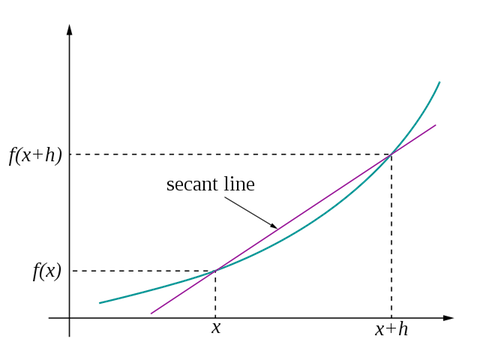
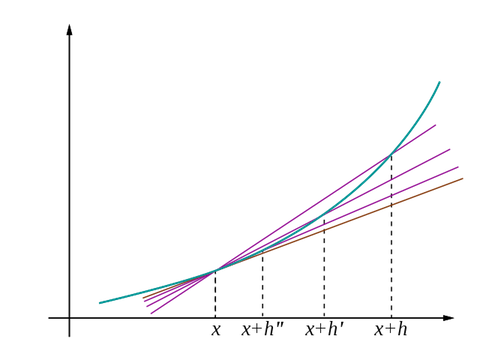
画像引用: 微分 - Wikipedia
これは f(x)のx=aにおける微分係数 と呼ばれます。
一般化すると以下の公式で表すことが出来ます。
$$
f’(x) = \lim_{h \to 0} \frac{f(x+h)-f(x)}{h}
$$
導関数(derivative)とは
微分係数が求められる関数を導関数 と言います。上の公式だとf’()で表される関数ですね。
導関数の表記法は以下の様に表すことが出来ます。
$$
f’(x) = y’
$$
分かり易い表記法なのですが、複数の変数をとる関数を微分するために以下の様な表し方があります。
$$
f’(x) = \frac{dy}{dx} = \frac{df(x)}{dx} = \frac{d}{dx} f(x)
$$
これは関数y=f(x)をxで微分する。という意味です。
機械学習の中で使われ方
機械学習の中で最急降下法(Gradient descent)というアルゴリズムを利用する場面が出てきます。
最急降下法(Gradient descent)は目的関数(cost function)の最小値を、傾きを使って算出する方法なのですが、この中で上記の導関数を利用します。(実際は変数を複数利用する「偏微分」)
$$
\theta_j := \theta_j - \alpha \frac{\partial}{\partial \theta_j} J(\theta_0, \theta_1)
$$
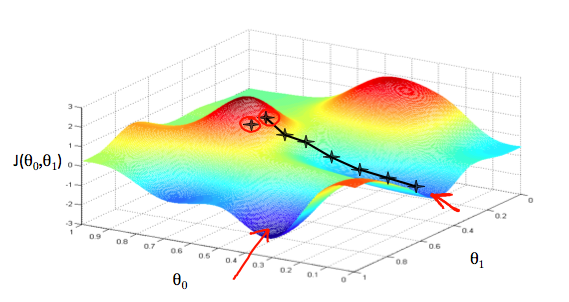
画像引用: Machine Learning - Coursera
このアルゴリズムの中に導関数が使われています。
$$
f’(x) = \frac{d}{dx} f(x)
$$
まとめ
最近初めた機械学習のオンライン講座 Machine Learning - Coursera で分かりづらかった微分に関して自分なりに整理してみました。
先は長いですが、機械学習・深層学習のアルゴリズムの理解が深まれば良いなと思います。では。