思い返せば去年の12月 以来、今ひとつ良く分からなかったがニューラルネットワークの仕組みでした。
Mchine Learning - Coursera がちょうどニューラルネットワークの章に入ったので、改めてその仕組みを考えてみたいと思います。
ロジスティック回帰 (Logistic Regression)
ロジスティック回帰を利用する事で分類問題を解く事が出来ますが、ニューラルネットワークを使う事の利点は何なのでしょうか?
改めて図でまとめてみます。
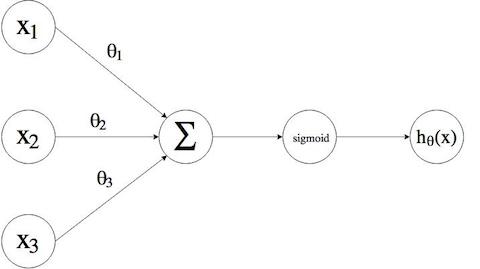
予測変数 $x$ を元にして 応用変数 $y = h_\theta(x)$ を推測します。
$\sum$(ループ)で二乗誤差法を用いて全ての点の誤差が最小であるパラメータ$\theta^T x$ を求め、シグモイド関数 $g(z) = \dfrac{1}{1 + e^{-z}}$ に代入する事で分類判定を行いました。
図を改めて見て分かったのですが、パラメータ $\theta$ はニューラルネットワークで言う所の「重み」 $w$ と同じなんですね。
ニューラルネットワークの順伝播
講座の中でのアンドリュー先生の説明が分かりやすかったのでまとめてみます。
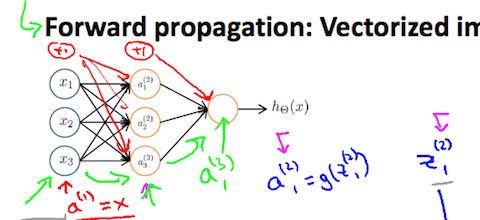
画像引用: Mchine Learning - Coursera
ニューラルネットワークの順伝播(フォワードプロパゲーション)はこの様な図で表わせます。
パラメータ $\Theta$ の伝播が複雑になりますので、出力層の一つ前の隠れ層を入力層と考えてみます。
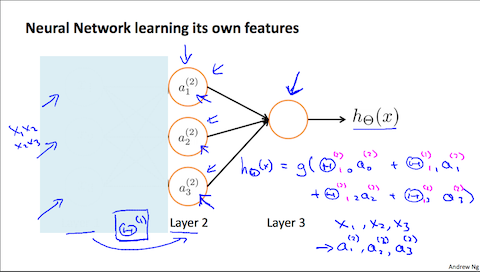
画像引用: Mchine Learning - Coursera
こんな感じになり、ロジスティック回帰と同じ形になります。以下講義内容の抜粋です。
これがやってる事は 単なるロジスティック回帰だ。ニューラルネットワークがやる事は ロジスティック回帰みたいなものだが、 もとの特徴量である $x_1$、$x_2$、$x_3$を使う代わりに新しい特徴量$a_1$、$a_2$、$a_3$を使うって所だけが違う。
これのクールな所は、特徴量 $a_1$、$a_2$、$a_3$,は それら自身が入力の関数として 学習された物である、という事だ。
複雑な特徴量を学習出来て結果として より良い仮説が 得られる。
多項式回帰を使い、複雑な曲線で分類する事は可能ですが、非線形分類(例:XORやXNORなどの論理演算)を行う事は出来ません。
ニューラルネットワークを利用する事で複雑な特徴量を学習出来て結果として より良い仮説が 得られる。という訳です。
ニューラルネットワークの仮説
引用画像の様な3層構造の仮説 $h_\Theta(x)$ は以下の様に表わせます。
$${ h_\Theta (x) = a_1 ^{(3)} = g(\Theta_{10} ^{(2)} a_0 ^{(2)} + \Theta_{11} ^{(2)} a_1 ^{(2)} + \Theta_{12} ^{(2)} a_2 ^{(2)} + \Theta_{13} ^{(2)} a_3 ^{(2)} + \Theta_{14} ^{(2)} a_4 ^{(2)} ) }$$ぱっと見た瞬間、根をあげそうになりますが、添え字を省略するとロジスティック回帰の仮説
$$
{
h_\theta (x) = g(\theta_0 x_0 + \theta_1 x_1 + \theta_3 x_3 + \theta_4 x_4)
}
$$
と同じであることが分かります。では。