さて、ニューラルネットワークの逆伝播法についてまとめてみます。
Machine Learning - Coursera 講義の中でアンドリュー先生はこんな風に言っています。
多くの人にとっては 最初に見たら 第一印象は 「うげぇ。こりゃすげー複雑な アルゴリズムだ! そしてこんなたくさんの ステップがあるなんて!」と。
あなたがバックプロパゲーションを、 もしそんな風に感じていたとしても、 実は問題ありません。
でも実の所、私も長年、ひょっとしたら今日ですら、 バックプロパゲーションが何やってるのか いまいち直感的に理解出来てないなぁ、と 思う事はあるけれど、 使う分には問題なく とてもしっかりと 使えてきました。
こんな気さくな語り口が人気の秘密ですね。
さて、そうは言いつつも逆伝播に関し出来る限り仕組みが理解できる様、図を使いながら説明されています。
ニューラルネットワークの順伝播
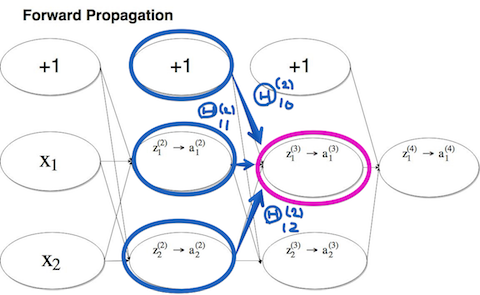
$(x^{(i)}, y^{(i)})$ である場合のニューラルネットワークの順伝播を見ていきます。
パラメータ(重み) $\Theta$ の総和が $z_j^{(l)}$ となり、活性化関数(ここではシグモイド関数)を適応した値が $a_j^{(l)}$ となります。
※実際の活性化関数はReLu関数を使われる事が多い様ですが、ここでは講座に則ってシグモイド関数で考えます。
前回記事 で見た様に、特徴量 $a_j^{(l)}$ を元にしたロジスティック回帰です。試しに $z_1^{(3)}$ のプロセスを見てみます。
$$z_1^{(3)} = \Theta_{10}^{(2)}×1+\Theta_{11}^{(2)}×a_1^{(2)}+\Theta_{11}^{(2)}×a_2^{(2)}$$こんな風に表わせます。さて、講義の中で逆伝播はこの順伝播と同じ様な計算であり、計算の流れが逆になっている事が異なると説明されます。
ニューラルネットワークの逆伝播
ここでは簡単の為出力層が一つで設定している為、目的関数を計算するのにループ処理や正則化を省いて考えます。
$$cost(i) = y^{(i)}log(h_\Theta(x^{(i)}))+ (1 - y^{(i)}) log(1-h_\Theta (x^{(i)}))$$つまり予測値 $i$ に対してのコストは以下の様に
$$
cost(i) ≈ (h_\theta(x^{(i)}-y^{(i)})^2)
$$
ニューラルネットワークの出力の値と実際の値における、目的関数の誤差の2乗(の様なものでる)と考えてみる。という事です。実際に図でみてみます。
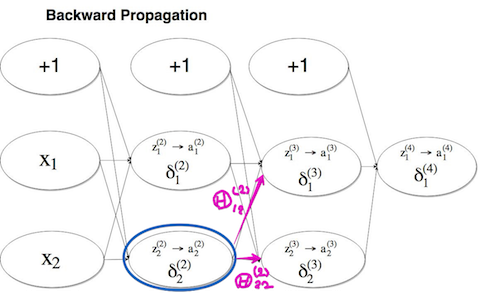
試しに $\delta_2^{(2)} $ のプロセスをみてみます。
$$\delta_2^{(2)} = \Theta_{12}^{(2)}×\delta_1^{(3)} + \Theta_{22}^{(2)}×\delta_2^{(3)}$$ここではバイアス $b$ は微分に影響しない為計算から除外しています。確かに順伝播と同じ様な計算をしている事が分かります。
上の順伝播の図にある $\Theta_{12}^{(2)} $ に対する、
下の逆伝播の $\Theta_{12}^{(2)} $ の二乗誤差を最急降下法などのアルゴリズムに代入する事で最小点を導く事が出来ます。
(多分。これで合ってるのだろうか…。)
備考:連鎖律(chain rule)- 複合関数の微分
さて、この講義では触れられませんでしたが(逆伝播に関してはOctaveを実装する事で理解を深める内容になっていました)、実際に誤差逆伝播法を計算するには連鎖律(chain rule)が必要になります。
$$
\frac{dz}{dx} = \frac{dz}{dt} ×\frac{dt}{dx}
$$
この計算式を用いることによって勾配の計算を早く行う事が出来ます。
参考にさせていただきました
Coursera Machine Learning (5): ニューラルネットワークとバックプロパゲーション - Qiita