さて、コーセラの機械学習講座も残り僅かになりました(先週はまとめブログサボっちゃっいましたが…)。今回は確率的最急降下法(SGD)について学びました。
今年のはじめ、ニューラルネットワークのライブラリKerasを使ったときに活性化関数をメソッドとして使いました。
|
|
こんな感じで指定します。その時は「損失をアルゴリズムによって減少させる」ものというざっくりとした理解でしたがもう少し理解を深めてみます。
確率的最急降下法 (Stochastic Gradient Descent)
第2週で学んだ、最急降下法はパラメータ $\theta$ を更新する際データ $m$ すべての誤差を計算することで目的関数 $J(\theta)$ の最小値を求めました。
これはバッジ最急降下法(Batch Gradient Descent)とも呼ばれます。この手法の問題点は大量のデータ処理する際、多くの時間が掛かってしまうことです。
そこで大量のデータを扱う際、パラメータ更新を全てのデータを使うのではなく1つのデータを $m$ 回更新するアルゴリズムを用いることで目的関数 $J(\theta)$ の最小値に近づける事ができます。
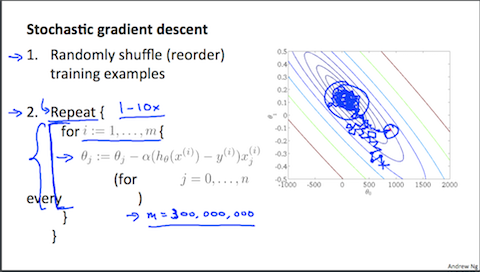
画像引用:Machine Learning - Coursera
最初にデータをシャッフルすることがポイントとなります。
バッジ最急降下法と違って最小値へ向かって勾配を下る動きは出来ないのですが、最小値の付近に次第に接近していきます。
ミニバッジ最急降下法(Mini-Batch Gradient Descent)
更新用のデータを1つではなく、合計 $m$ 個のうち $b$ 個使用するアルゴリズムをミニバッジ最急降下法といいます。
収束が上手く行えない際は学習率 $\alpha$ を小さくし、確実に収束させるためにはリピート回数を増やすごとに学習率を小さくなるように設計します。