ちょっと前まで「教師なし学習」と聞いて、機械が自分で学習して知識を身につける AlphaGo Zero みたいなやつを想像していました。ポンダッドです。
さて、Coursera Machine Learning 8週目は「教師なし学習」の講義でした。クラスタリング (Clustering)と呼ばれる正解ラベルのないデータを元に似たグループをまとめる手法です。
K-means(k平均法)
まずはグラフを見ていきましょう。
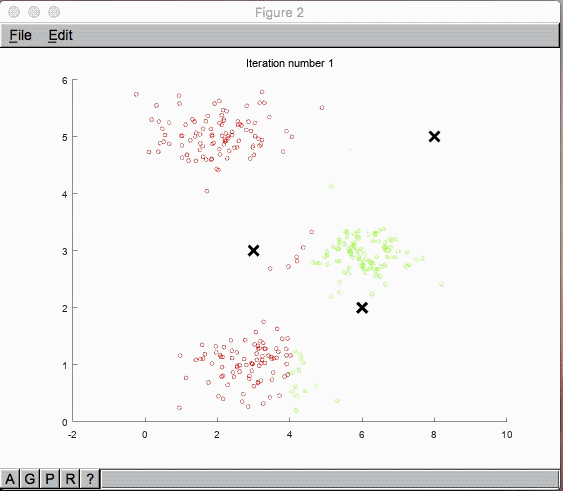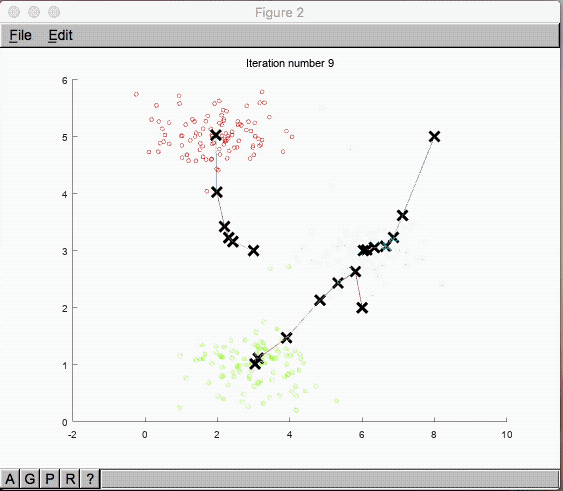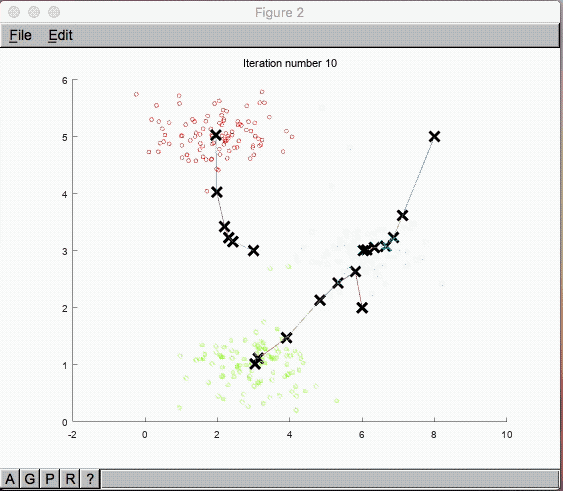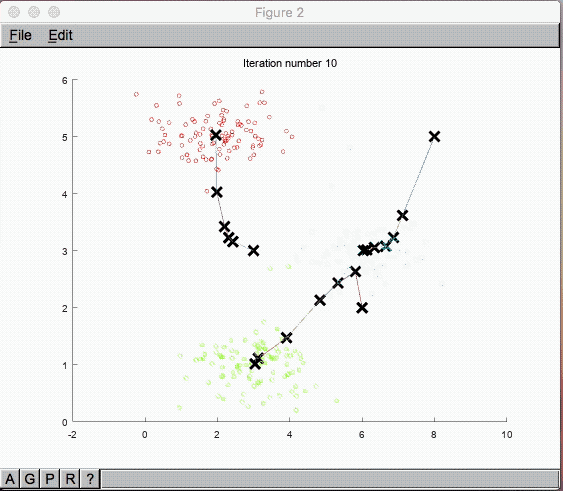
回帰分析の目的関数を最急降下法で算出している形に似ており、イメージはしやすそうな感じです。
ただ正解ラベルと推測の誤差(二乗誤差)の最小値を求めるのとは違い、これらのデータ群に特に正解ラベルはありません。
どうやって似たグループを見つけているのでしょうか?
「教師なし」とはいえ、グループ分けする数は $K$ 個のクラスタリングとして予め指定します。
その中心点として $\mu_1, \mu_2,…, \mu_K$ をまずはランダムに指定します。
データ群 $x^{(i)}$ のラベルは $K$ 個になりますが、
これら$x^{(i)}$ は$\mu_1, \mu_2,…, \mu_K$ の中で一番近いものにクラスタリングされます。
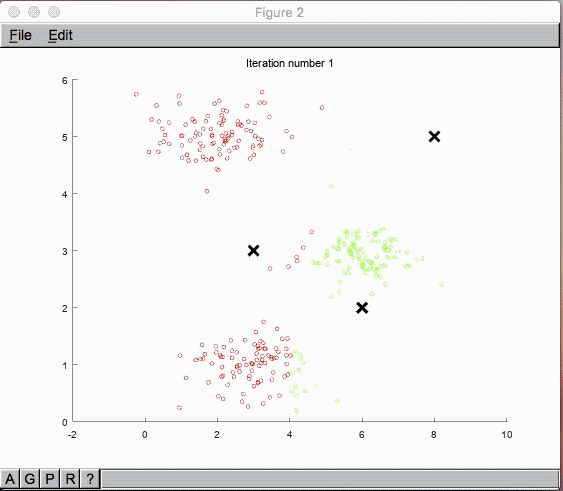
ここから中心点 $\mu_1, \mu_2,…, \mu_K$ を更新していきます。新しい中心点はクラスタリングされた $x^{(i)}$ と $\mu$ の平均値に更新されていきます。
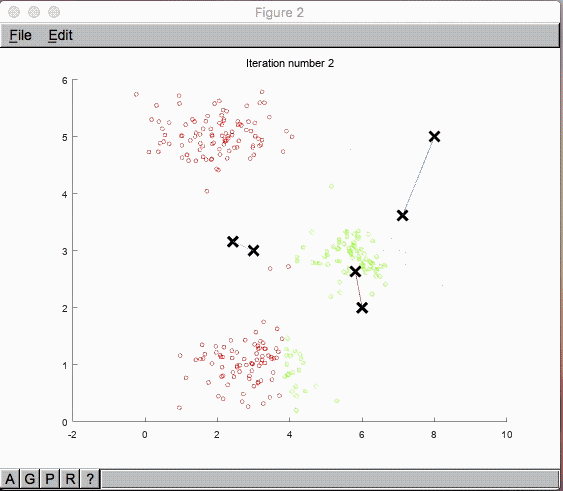
これを繰り返せば上手くクラスタリングされていきそうですが、どれ位繰り返せば良いのでしょうか?
これは回帰分析と同様に二乗誤差を用いて目的関数の最適化を図ります。
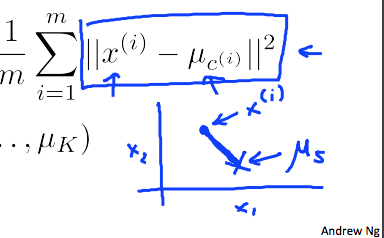
画像引用:Machine Learning - Coursera
数式で表すと以下の様に表せます。
$${ J(c^{(1)},...,c^{(m)},\mu_1,...,\mu_K) = \frac{1}{m} \sum^m_{i=1} ||x^{(i)} - \mu_{c^{(i)}}||^2 }$$以上です。
参考にさせていただきました
Coursera Machine Learning (8): 教師なし学習 (K-Means)、主成分分析 (PCA) - Qiita