前回 誤差逆伝播法の詳細を見ていきたいと思います、と書きました。人工知能愛好家(Artificial Intelligence Hobbyist)ポンダッドです。
さらりとそんなことを書きましたが、そんなに甘いものではなく何度も何度も繰り返して講座を復習してみましたものの、しっかりと理解できたとは言い難い状況です。
ふわっとした理解で恐縮ですが、まとめてみます。
浅いニューラルネットワーク(Shallow neural networks)
ディープラーニングを見る前にまずは隠れ層が1層となるニューラルネットワークを考えていきます。
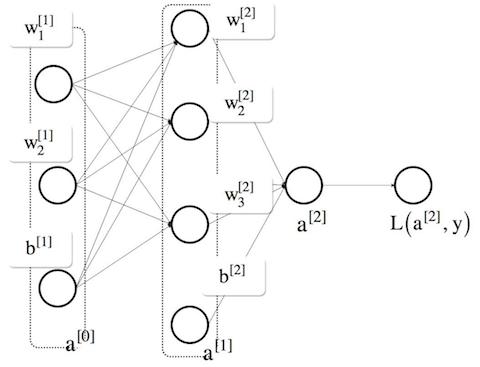
図で表すとこんな感じです。$m$ 個の学習データの特徴量 $X$ を元にラベル $y$ と学習した結果 $\hat{y}$ (ここでは $a^{[2]}$ )であることを示します。
損失関数を $\mathcal{L}$ としていますので、その最小値を求めていくことが目的となります。
前回ロジスティック回帰の最急降下法をまとめました。隠れ層が増えることでその逆伝播にどんな変化が現れるのでしょうか?
誤差逆伝播法(Backpropagation )
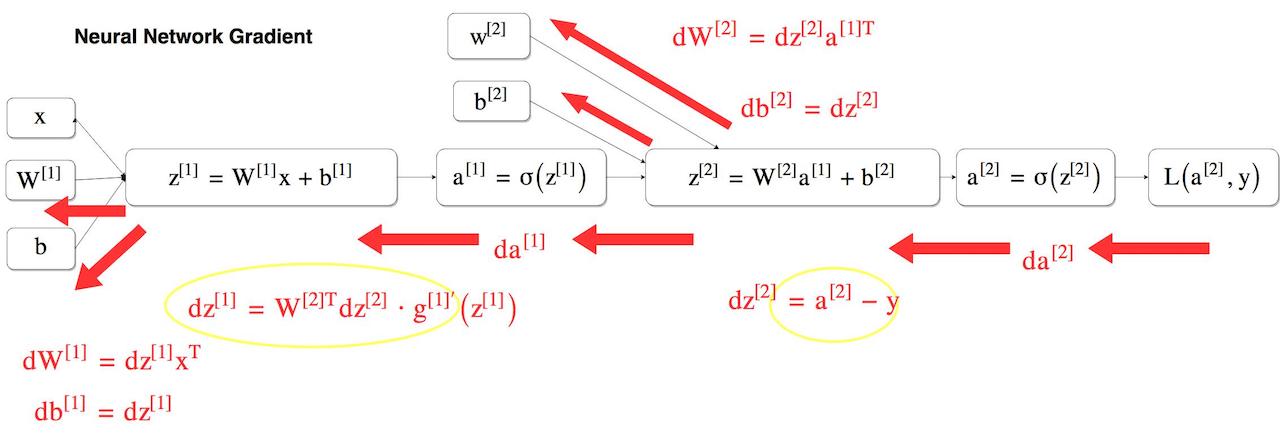
上の図を計算グラフで書き直すとこのようになります。重み $W$ が大文字になっているのがポイントです。重み $w$ を配列に格納したものです。
これも計算リソースを削減させる工夫のひとつです。膨大なデータをひとつひとつループ処理を使って計算するのでは無く行列を使い一気に計算していきます。
機械学習講座の ニューラルネットワークの順伝播 でまとめたように、ディープラーニングの出力層(分類の場合)はロジスティック回帰と同じ形になります。
誤差逆伝播法を利用する場合でも、
$$
dz^{[2]} = a^{[2]} - y
$$
という逆伝播の微分式は同じ形になります。(図の右黄色い丸部分)
連鎖率によって導き出す式ですが、出来過ぎな位良くできています。これは、計算結果 $a^{[2]}$ とラベル $y$ の誤差と全く一緒です。
あまりにも整いすぎていて不思議だったのですが、これは「そのように設計しているから」という事の様です。すごいよ!
さて、ここからが最大のポイントです。隠れ層の微分は以下の様になります。(図の左黄色い丸部分)
$$
dz^{[1]} = W^{[2]T}dz^{[2]} * g^{[1]’}(z^{[1]})
$$
あれ、なんか予想と違う(出力層と形が違う)。
これは合成関数の処理の仕方が違うので形が変わっています。「連鎖律の原理」により$dz$ はこんな式で表せます。
$$
\frac{dL}{dz} = \frac{dL}{da} \frac{da}{dz}
$$
この式を右の $dz^{[1]}$ にあてはめてみます。$\frac{da}{dz}$ はシグモイド関数の微分 $g^{[1]’}(z^{[1]})$ として表せます。
そうするとのこりの $\frac{dL}{da} $ (省略すると $da$ )は…
隣りにある $da^{[1]}$ になります。ちょっと引用してみます。
行列(多次元配列)を対象とした逆伝播を求める場合は、行列の要素ごとに書き下すことで、スカラ値を対象とした計算グラフと同じ手順で考えることが出来ます。実際に書き下してみると次の式が得られます
$$
\frac{dL}{dW} = X^{[T]} \frac{dL}{dY}
$$式の $W^{[T]}$ の $T$ は転置を表します。
ゼロから作るDeep Learning - O’REILLYジャパン
この式と同じです。$X$ は配列なので、転置するとちょうど上の図のように行列の形になります。
最急降下法
機械学習講座のニューラルネットワークの逆伝播 では目的関数の誤差を二乗誤差(のようなもの)で最小値をもとめる、と考えました。実際どのように計算するのでしょう。

画像引用:Neural networks and Deep learning - Coursera
計算グラフで考えた微分を使い二乗誤差(のようなもの)で最小値を求めていきます。計算式で表すよりもNumPy形式で考えたほうが分かりやすそうですね。
…ふう。自分の理解力の限界を超えてしまいました。ふわっとしていますが今日はここまで。