さて、機械学習講座を粛々と受講してきたのですが、ようやく6週目が終わり折り返し地点に来ました。(長いな)
今週は機械学習のアルゴリズム精度を高めるための手法を学びました。今回はオーバーフィッティング、アンダーフィッティングをどのように避けるのかについてまとめてみます。
仮説の評価
仮説を評価するための訓練用データセットは、トレーニングセット70%、テストセット30%で構成するのが一般的であり、それによってエラー率を測ります。
多項式回帰でより精度を上げる際、トレーニングセット60%、交差検定 (Cross Validation)セット20%、テストセット20%でデータセットを構成し、一般化エラー率をさせることが出来ます。
正則化パラメーター $λ$(ラムダ)
さて、前々々回 正則化パラメーター $λ$(ラムダ)を使うことを学びました。
$${ J(\theta) = \frac{1}{2m} \sum_{i=1}^m (h_\theta (x^{(i)}) - y^{(i)})^2 + \lambda \sum_{j=1}^n \theta_j^2 }$$$λ$(ラムダ)によりオーバーフィッティング、アンダーフィッティングを調整し、適正な正則化が行うことが出来ます。
バイアス (Bias )とバリアンス(Variance)
講義の中で、オーバーフィッティング(高バリアンス)、アンダーフィッティング(高バイアス)を解消するため$λ$(ラムダ)の最小値を得る手法を解説しています。
- バイアス (Bias)日本語では「偏り」平均値の大きさ
- バリアンス(Variance)日本語では「分散」最大値 - 最小値の大きさ
「分散」が大きい → 多項式回帰の次元が大きい。「偏り」が大きい → 多項式回帰の次元が小さい。とも言えます。
では、 $λ$(ラムダ)の値はどのように選択すれば良いのでようか?
講義の中では手動で計算する方法として $λ$(ラムダ)の値を10個程度設定し、トレーニングセットと交差検定セットに対する目的関数が一番接近する値を抽出する手法が説明されていました。
※ $λ$(ラムダ)の数値は0.01、0.02、0.04…の様に2倍づつ進めてある程度の大きさまで(ここでは10.24)進めるとのこと。
図で表すと以下の様になります。
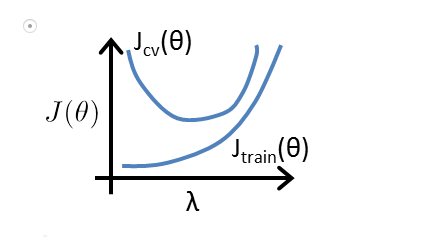
画像引用:Machine Learning - Coursera
こういった手法を使うことで、オーバーフィッティング、アンダーフィッティングがどれ位起きているか客観的な指標を得ることが出来るという訳です。
意思決定のプロセス
講座の中で次の様にまとめられていますので転記します。
- より多くの訓練用データセット → オーバーフィッティング(高バリアンス)を修正する
- トレーニングセットの特徴量の数を減らす → オーバーフィッティング(高バリアンス)を修正する
- トレーニングセットの特徴量の数を増やす → アンダーフィッティング(高バイアス)を修正する
- 多項式の項を増やす → アンダーフィッティング(高バイアス)を修正する
- $λ$ を小さくする → アンダーフィッティング(高バイアス)を修正する
- $λ$ を大きくする → オーバーフィッティング(高バリアンス)を修正する
今日はここまで。では。
参考にさせていただきました
Coursera Machine Learning (6): 機械学習のモデル評価(交差検定、Bias & Variance、適合率 & 再現率)- Qiita